Array Modes Tutorial
Introduction
As described in Lecture 5, the 4D-Var state-vector increments can be expressed as a weighted sum of the array modes:
where () are the eigenpairs of the preconditioned stabilized representer matrix (). The array modes corresponding to the largest eigenvalue represents the interpolation patterns for the observations that are most stable with respect to changes in the innovation vector d, since the array modes depend only on the observation locations and not on the observation values.
Model Set-up
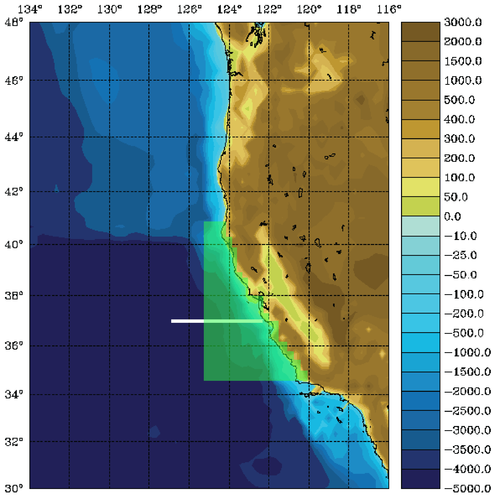
The WC13 model domain is shown in Fig. 1 and has open boundaries along the northern, western, and southern edges of the model domain.
In the tutorial, you will perform a 4D-Var data assimilation cycle that spans the period 3-6 January, 2004. The 4D-Var control vector δz is comprised of increments to the initial conditions, δx(t0), surface forcing, δf(t), and open boundary conditions, δb(t). The prior initial conditions, xb(t0), are taken from the sequence of 4D-Var experiments described by Moore et al. (2011b) in which data were assimilated every 7 days during the period July 2002- December 2004. The prior surface forcing, fb(t), takes the form of surface wind stress, heat flux, and a freshwater flux computed using the ROMS bulk flux formulation, and using near surface air data from COAMPS (Doyle et al., 2009). Clamped open boundary conditions are imposed on (u,v) and tracers, and the prior boundary conditions, bb(t), are taken from the global ECCO product (Wunsch and Heimbach, 2007). The free-surface height and vertically integrated velocity components are subject to the usual Chapman and Flather radiation conditions at the open boundaries. The prior surface forcing and open boundary conditions are provided daily and linearly interpolated in time. Similarly, the increments δf(t) and δb(t) are also computed daily and linearly interpolated in time.
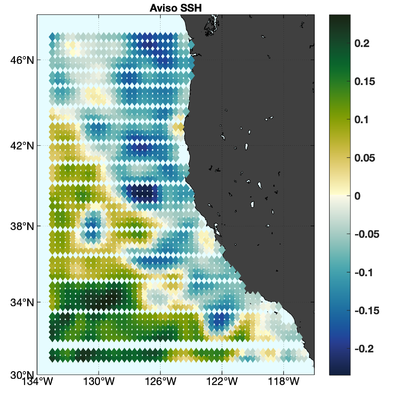
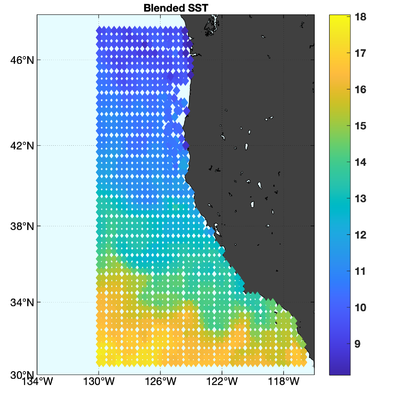
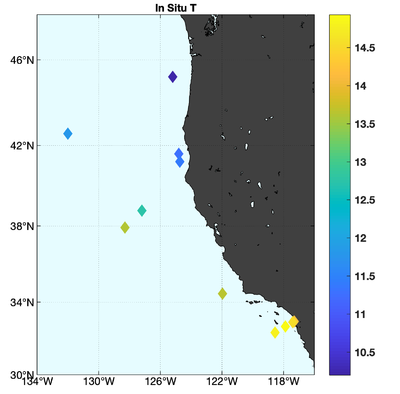
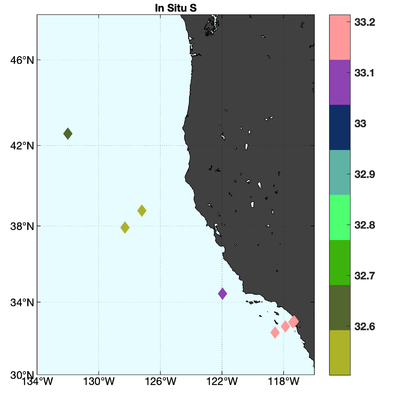
The observations assimilated into the model are satellite SST, satellite SSH in the form of a gridded product from Aviso, and hydrographic observations of temperature and salinity collected from Argo floats and during the GLOBEC/LTOP and CalCOFI cruises off the coast of Oregon and southern California, respectively. The observation locations are illustrated in Fig. 2.
 |
 |
 |
 |
Running the Array Modes Driver
To compute the array modes, you must first run RBL4D-Var because the array mode driver will use the Lanczos vectors generated by your dual 4D-Var calculation.
To run this exercise, go first to the directory WC13/ARRAY_MODES, and follow the directions in the Readme file. The only change that you need to make is to s4dvar.in, where you will select the array mode that you wish to calculate (you may only calculate on mode at a time). The choice of array mode is determined by the parameter Nvct. The array modes are referenced in reverse order, so choosing Nvct=Ninner-1 is the array mode with the second largest eigenvalue, and so on. Note that Nvct must be assigned a numeric value (i.e. Nvct=10 for the 4D-PSAS tutorial).
Important CPP Options
The following C-preprocessing options are activated in the build script:
ANA_SPONGE Analytical enhanced viscosity/diffusion sponge
ARRAY_MODES_SPLIT Analysis due to IC, surface forcing, and OBC
RPCG Restricted B-preconditioned Lanczos minimization
SKIP_NLM Skipping running NLM, reading NLM state trajectory
WC13 Application CPP option
Input NetCDF Files
WC13 requires the following input NetCDF files:
Nonlinear Initial File: wc13_ini.nc
Forcing File 01: ../Data/coamps_wc13_lwrad_down.nc
Forcing File 02: ../Data/coamps_wc13_Pair.nc
Forcing File 03: ../Data/coamps_wc13_Qair.nc
Forcing File 04: ../Data/coamps_wc13_rain.nc
Forcing File 05: ../Data/coamps_wc13_swrad.nc
Forcing File 06: ../Data/coamps_wc13_Tair.nc
Forcing File 07: ../Data/coamps_wc13_wind.nc
Boundary File: ../Data/wc13_ecco_bry.nc
Adjoint Sensitivity File: wc13_ads.nc
Initial Conditions STD File: ../Data/wc13_std_i.nc
Model STD File: ../Data/wc13_std_m.nc
Boundary Conditions STD File: ../Data/wc13_std_b.nc
Surface Forcing STD File: ../Data/wc13_std_f.nc
Initial Conditions Norm File: ../Data/wc13_nrm_i.nc
Model Norm File: ../Data/wc13_nrm_m.nc
Boundary Conditions Norm File: ../Data/wc13_nrm_b.nc
Surface Forcing Norm File: ../Data/wc13_nrm_f.nc
Observations File: wc13_obs.nc
Lanczos Vectors File: wc13_lcz.nc
Various Scripts and Include Files
The following files will be found in WC13/ARRAY_MODES directory after downloading from ROMS test cases SVN repository:
Readme instructions
build_roms.csh csh Unix script to compile application
build_roms.sh bash shell script to compile application
job_array_modes.sh job configuration script
roms_wc13.in ROMS standard input script for WC13
s4dvar.in 4D-Var standard input script template
wc13.h WC13 header with CPP options
Instructions
To run this application you need to take the following steps:
- We need to run the model application for a period that is long enough to compute meaningful circulation statistics, like mean and standard deviations for all prognostic state variables (zeta, u, v, T, and S). The standard deviations are written to NetCDF files and are read by the 4D-Var algorithm to convert modeled error correlations to error covariances. The error covariance matrix, D=diag(Bx, Bb, Bf, Q), is very large and not well known. B is modeled as the solution of a diffusion equation as in Weaver and Courtier (2001). Each covariance matrix is factorized as B = K Σ C ΣT KT, where C is a univariate correlation matrix, Σ is a diagonal matrix of error standard deviations, and K is a multivariate balance operator.In this application, we need standard deviations for initial conditions, surface forcing (ADJUST_WSTRESS and ADJUST_STFLUX), and open boundary conditions (ADJUST_BOUNDARY). If the balance operator is activated (BALANCE_OPERATOR and ZETA_ELLIPTIC), the standard deviations for the initial and boundary conditions error covariance are in terms of the unbalanced error covariance (K Bu KT). The balance operator imposes a multivariate constraint on the error covariance such that the unobserved variable information is extracted from observed data by establishing balance relationships (i.e., T-S empirical formulas, hydrostatic balance, and geostrophic balance) with other state variables (Weaver et al., 2005). The balance operator is not used in the tutorial.The standard deviations for WC13 have already been created for you:../Data/wc13_std_i.nc initial conditions
../Data/wc13_std_b.nc open boundary conditions
../Data/wc13_std_f.nc surface forcing (wind stress and net heat flux) - Since we are modeling the error covariance matrix, D, we need to compute the normalization coefficients to ensure that the diagonal elements of the associated correlation matrix C are equal to unity. There are two methods to compute normalization coefficients: exact and randomization (an approximation).The exact method is very expensive on large grids. The normalization coefficients are computed by perturbing each model grid cell with a delta function scaled by the area (2D state variables) or volume (3D state variables), and then by convolving with the squared-root adjoint and tangent linear diffusion operators.The approximate method is cheaper: the normalization coefficients are computed using the randomization approach of Fisher and Courtier (1995). The coefficients are initialized with random numbers having a uniform distribution (drawn from a normal distribution with zero mean and unit variance). Then, they are scaled by the inverse squared-root of the cell area (2D state variable) or volume (3D state variable) and convolved with the squared-root adjoint and tangent diffusion operators over a specified number of iterations, Nrandom.Check following parameters in the 4D-Var input script s4dvar.in (see input script for details):Nmethod == 0 ! normalization method: 0=Exact (expensive) or 1=Approximated (randomization)These normalization coefficients have already been computed for you (../Normalization) using the exact method since this application has a small grid (54x53x30):
Nrandom == 5000 ! randomization iterations
LdefNRM == T T T T ! Create a new normalization files
LwrtNRM == T T T T ! Compute and write normalization
CnormM(isFsur) = T ! model error covariance, 2D variable at RHO-points
CnormM(isUbar) = T ! model error covariance, 2D variable at U-points
CnormM(isVbar) = T ! model error covariance, 2D variable at V-points
CnormM(isUvel) = T ! model error covariance, 3D variable at U-points
CnormM(isVvel) = T ! model error covariance, 3D variable at V-points
CnormM(isTvar) = T T ! model error covariance, NT tracers
CnormI(isFsur) = T ! IC error covariance, 2D variable at RHO-points
CnormI(isUbar) = T ! IC error covariance, 2D variable at U-points
CnormI(isVbar) = T ! IC error covariance, 2D variable at V-points
CnormI(isUvel) = T ! IC error covariance, 3D variable at U-points
CnormI(isVvel) = T ! IC error covariance, 3D variable at V-points
CnormI(isTvar) = T T ! IC error covariance, NT tracers
CnormB(isFsur) = T ! BC error covariance, 2D variable at RHO-points
CnormB(isUbar) = T ! BC error covariance, 2D variable at U-points
CnormB(isVbar) = T ! BC error covariance, 2D variable at V-points
CnormB(isUvel) = T ! BC error covariance, 3D variable at U-points
CnormB(isVvel) = T ! BC error covariance, 3D variable at V-points
CnormB(isTvar) = T T ! BC error covariance, NT tracers
CnormF(isUstr) = T ! surface forcing error covariance, U-momentum stress
CnormF(isVstr) = T ! surface forcing error covariance, V-momentum stress
CnormF(isTsur) = T T ! surface forcing error covariance, NT tracers fluxes../Data/wc13_nrm_i.nc initial conditionsNotice that the switches LdefNRM and LwrtNRM are all false (F) since we already computed these coefficients.
../Data/wc13_nrm_b.nc open boundary conditions
../Data/wc13_nrm_f.nc surface forcing (wind stress and
net heat flux)The normalization coefficients need to be computed only once for a particular application provided that the grid, land/sea masking (if any), and decorrelation scales (HdecayI, VdecayI, HdecayB, VdecayV, and HdecayF) remain the same. Notice that large spatial changes in the normalization coefficient structure are observed near the open boundaries and land/sea masking regions. - Before you run this application, you need to run the standard RBL4D-Var (../RBL4DVAR directory) since we need the Lanczos vectors. Notice that in job_array_modes.sh we have the following operation:cp -p ${Dir}/RBL4DVAR/EX3_RPCG/wc13_mod.nc wc13_lcz.ncIn R4D-Var (observartion space minimization), the Lanczos vectors are stored in the output 4D-Var NetCDF file wc13_mod.nc.
- Customize your preferred build script and provide the appropriate values for:
- Root directory, MY_ROOT_DIR
- ROMS source code, MY_ROMS_SRC
- Fortran compiler, FORT
- MPI flags, USE_MPI and USE_MPIF90
- Path of MPI, NetCDF, and ARPACK libraries according to the compiler are set in my_build_paths.csh. Notice that you need to provide the correct places of these libraries for your computer. If you want to ignore this section, set USE_MY_LIBS value to no.
- Notice that the most important CPP options for this application are specified in the build script instead of wc13.h:setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DARRAY_MODES"This is to allow flexibility with different CPP options.
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DANA_SPONGE"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DARRAY_MODES_SPLIT"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DRPCG"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DSKIP_NLM"For this to work, however, any #undef directives MUST be avoided in the header file wc13.h since it has precedence during C-preprocessing. - You MUST use the build script to compile.
- Customize the ROMS input script roms_wc13.in and specify the appropriate values for the distributed-memory partition. It is set by default to:Notice that the adjoint-based algorithms can only be run in parallel using MPI. This is because of the way that the adjoint model is constructed.
- Customize the configuration script job_array_modes.sh and provide the appropriate place for the substitute Perl script:set SUBSTITUTE=${ROMS_ROOT}/ROMS/Bin/substituteThis script is distributed with ROMS and it is found in the ROMS/Bin sub-directory. Alternatively, you can define ROMS_ROOT environmental variable in your .cshrc login script. For example, I have:setenv ROMS_ROOT /home/arango/ocean/toms/repository/trunk
- Execute the configuration job_array_modes.sh before running the model. It copies the required files and creates rbl4dvar.in input script from template s4dvar.in. This has to be done every time that you run this application. We need a clean and fresh copy of the initial conditions and observation files since they are modified by ROMS during execution.
- Run ROMS with data assimilation:mpirun -np 8 romsM roms_wc13.in > & log &
- We recommend creating a new subdirectory EX7, and saving the solution in it for analysis and plotting to avoid overwriting solutions when playing with different parameters. For examplemkdir EX7where log is the ROMS standard output specified in the previous step.
mv Build_roms rbl4dvar.in *.nc log EX7
cp -p romsM roms_wc13.in EX7
Plotting your Results
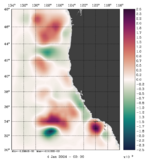
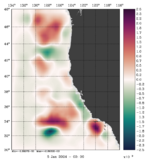
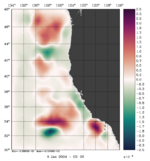
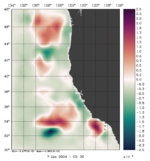
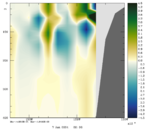
To plot a selection of fields for your chosen array mode, use the Matlab script plotting/plot_array_modes.m or ROMS plotting package script plotting/ccnt_array_modes.in for horizontal plots at 100 m or plotting/csec_array_modes.in for cross-sections along 37°N.
Results
The array modes spectrum of RBL4D-Var analysis of Exercise 3 with RPCG is plotted using plotting/plot_array_modes_spectrum.m. The dash line is the 1 percent rule (Bennett and McIntosh, 1984), array modes below the dash line are noisy and deteriorate the 4D-Var analysis because the over fitting of the model to the data. The figure indicates that the optimal number of inner loops for this application is (Ninner) is between 21 or 22. The array modes with the lowest eigenvalue has the lowest weight to the 4D-Var increment. Higher array modes after crossing the 1 percent rule will augment the uncertainties in the 4D-Var increments.
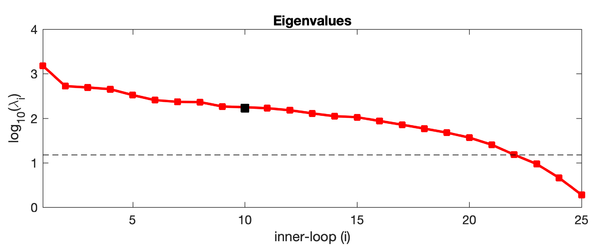
Notice that the plots below are the eigenvectors of the 10th inner-loop eigenvalue (Nvct = 10) shown by the black square.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |



