4DVar Normalization Tutorial
Introduction
In this tutorial you will compute the 4D-Var error covariance (D) normalization factors for the California Current System application WC13.
The error covariance matrix, D=diag(Bx, Bb, Bf, Q), is very large and not well known. B and Q are modeled as the solution of a diffusion equation following Weaver and Courtier (2001) methodology. Each covariance matrix is factorized as B = K Σ C ΣT KT, where C is a univariate correlation matrix, Σ is a diagonal matrix of error standard deviations, and K is a multivariate balance operator. The normalization coefficients are needed to ensure that the diagonal elements of the associated correlation matrix C are equal to unity.
There are two methods to compute the error covariance normalization coefficients: exact and randomization (an approximation).
The exact method is very expensive on large grids. The normalization coefficients are computed by perturbing each model grid cell with a delta function scaled by the area (2D state variables) or volume (3D state variables), and then by convolving with the squared-root adjoint and tangent linear diffusion operators.
In the cheaper approximate method, the normalization coefficients are computed using the randomization approach of Fisher and Courtier (1995). The coefficients are initialized with random numbers having a uniform distribution (drawn from a normal distribution with zero mean and unit variance). Then, they are scaled by the inverse squared-root of the cell area (2D state variable) or volume (3D state variable) and convolved with the squared-root adjoint and tangent diffusion operators over a specified number of iterations, Nrandom.
Since the grid for WC13 is relatively small, the error covariance normalization coefficients are computed using the exact method. They need to be computed only once for a particular application provided that the grid, land/sea masking (if any), and decorrelation scales remain the same.
Model Set-up
The WC13 model domain is shown in Fig. 1 and has open boundaries along the northern, western, and southern edges of the model domain.
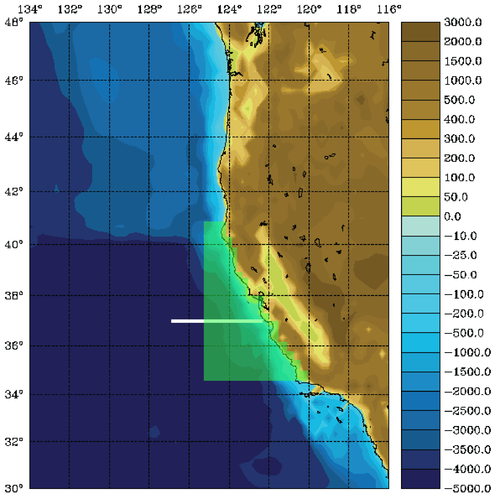
In the tutorial, you will perform a 4D-Var data assimilation cycle that spans the period 3-6 January, 2004. The 4D-Var control vector δz is comprised of increments to the initial conditions, δx(t0), surface forcing, δf(t), and open boundary conditions, δb(t). The prior initial conditions, xb(t0), are taken from the sequence of 4D-Var experiments described by Moore et al. (2011b) in which data were assimilated every 7 days during the period July 2002- December 2004. The prior surface forcing, fb(t), takes the form of surface wind stress, heat flux, and a freshwater flux computed using the ROMS bulk flux formulation, and using near surface air data from COAMPS (Doyle et al., 2009). Clamped open boundary conditions are imposed on (u,v) and tracers, and the prior boundary conditions, bb(t), are taken from the global ECCO product (Wunsch and Heimbach, 2007). The free-surface height and vertically integrated velocity components are subject to the usual Chapman and Flather radiation conditions at the open boundaries. The prior surface forcing and open boundary conditions are provided daily and linearly interpolated in time. Similarly, the increments δf(t) and δb(t) are also computed daily and linearly interpolated in time.
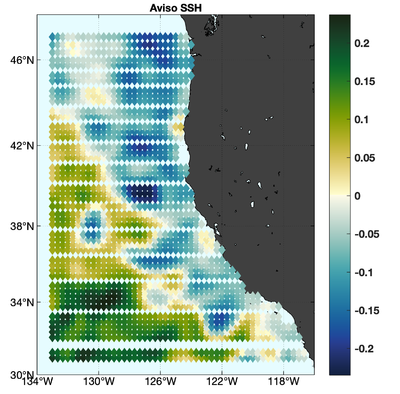
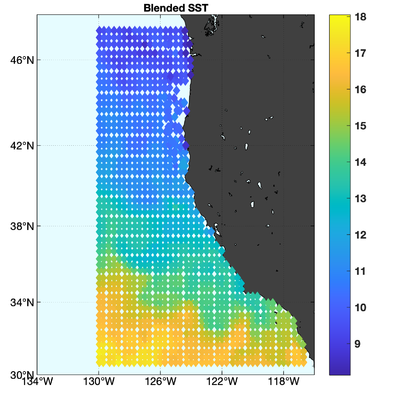
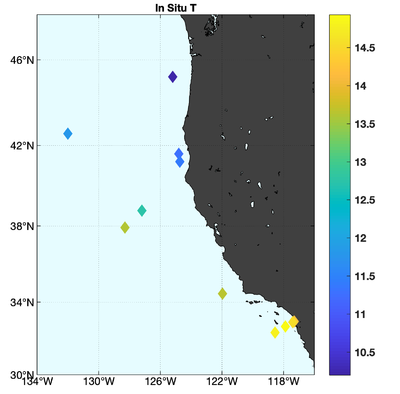
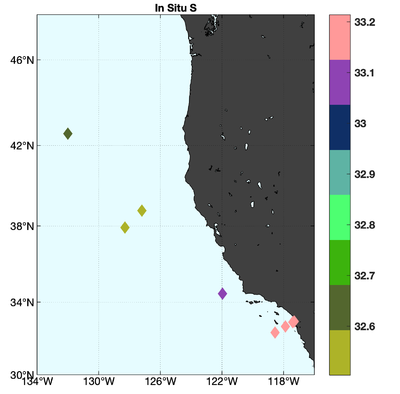
The observations assimilated into the model are satellite SST, satellite SSH in the form of a gridded product from Aviso, and hydrographic observations of temperature and salinity collected from Argo floats and during the GLOBEC/LTOP and CalCOFI cruises off the coast of Oregon and southern California, respectively. The observation locations are illustrated in Fig. 2.
 |
 |
 |
 |
Running 4D-Var Error Covariance Normalization
To run this tutorial, go first to the directory WC13/Normalization. Instructions for compiling and running the model are provided below or can be found in the Readme file. The roms_wc13.in input script is configured for this exercise.
Important CPP Options
The following C-preprocessing options are activated in the build script:
ADJUST_BOUNDARY Including boundary conditions in 4DVar state estimation
ADJUST_STFLUX Including surface tracer flux in 4DVar state estimation
ADJUST_WSTRESS Including surface wind stress in 4DVar state estimation
ANA_INITIAL Analytical initial conditions
WC13 Application CPP option
Input NetCDF Files
WC13 requires the following input NetCDF files:
Initial Conditions STD File: ../Data/wc13_std_i.nc
Model STD File: ../Data/wc13_std_m.nc
Boundary Conditions STD File: ../Data/wc13_std_b.nc
Surface Forcing STD File: ../Data/wc13_std_f.nc
Output NetCDF Files
The following output NetCDF files will be created containing the error covariance normalization coefficients:
Model Norm File: wc13_nrm_m.nc
Boundary Conditions Norm File: wc13_nrm_b.nc
Surface Forcing Norm File: wc13_nrm_f.nc
Various Scripts and Include Files
The following files will be found in WC13/Normalization directory after downloading from ROMS test cases SVN repository:
build_roms.csh csh Unix script to compile application
build_roms.sh bash shell script to compile application
job_normalization.csh job configuration script
roms_wc13.in ROMS standard input script for WC13
s4dvar.in 4D-Var standard input script template
wc13.h WC13 header with CPP options
Check these files for detailed information.
Important Parameters
Check following parameters in the 4D-Var input script s4dvar.in (see input script for details):
Nrandom == 5000 ! randomization iterations
LdefNRM == T T T T ! Create a new normalization files
LwrtNRM == T T T T ! Compute and write normalization
CnormM(isFsur) = T ! model error covariance, 2D variable at RHO-points
CnormM(isUbar) = T ! model error covariance, 2D variable at U-points
CnormM(isVbar) = T ! model error covariance, 2D variable at V-points
CnormM(isUvel) = T ! model error covariance, 3D variable at U-points
CnormM(isVvel) = T ! model error covariance, 3D variable at V-points
CnormM(isTvar) = T T ! model error covariance, NT tracers
CnormI(isFsur) = T ! IC error covariance, 2D variable at RHO-points
CnormI(isUbar) = T ! IC error covariance, 2D variable at U-points
CnormI(isVbar) = T ! IC error covariance, 2D variable at V-points
CnormI(isUvel) = T ! IC error covariance, 3D variable at U-points
CnormI(isVvel) = T ! IC error covariance, 3D variable at V-points
CnormI(isTvar) = T T ! IC error covariance, NT tracers
CnormB(isFsur) = T ! BC error covariance, 2D variable at RHO-points
CnormB(isUbar) = T ! BC error covariance, 2D variable at U-points
CnormB(isVbar) = T ! BC error covariance, 2D variable at V-points
CnormB(isUvel) = T ! BC error covariance, 3D variable at U-points
CnormB(isVvel) = T ! BC error covariance, 3D variable at V-points
CnormB(isTvar) = T T ! BC error covariance, NT tracers
CnormF(isUstr) = T ! surface forcing error covariance, U-momentum stress
CnormF(isVstr) = T ! surface forcing error covariance, V-momentum stress
CnormF(isTsur) = T T ! surface forcing error covariance, NT tracers fluxes
In large grid applications, you can accelerate computations by adjusting the above switches to submit several simultaneous jobs to compute the normalization coefficients for each state variables separately. Of course, you will need a lot of computer processors. If you use this strategy, make sure that the LdefNRM(:) switch is T for the first job and F for the other jobs. That is, we create the output normalization NetCDF file for initial conditions LdefNRM(1), model error LdefNRM(2), open boundary conditions LdefNRM(3), and surface forcing LdefNRM(4) only once in the first job. The other jobs only compute and write the specified state variable(s) error covariance normalization coefficient(s). Usually, the normalization coefficients for 2D state variables are computed quickly. However, the ones for 3D state variables are much slower as the number of vertical levels increase. If the spatial decorrelation scales for all tracer variables are the same, the algorithm computes the normalization coefficients for the first tracer (temperature) and assign the same values for the other tracers (salinity, etc).
Since this application has a small grid (54x53x30), this tutorial computes the normalization coefficients using the exact method or randomization methos, and creates the following files:
wc13_nrm_m.nc model error (weak constraint)
wc13_nrm_b.nc open boundary conditions
wc13_nrm_f.nc surface forcing (wind stress and net heat flux)
Notice that the switches LdefNRM and LwrtNRM are all true (T) so the model will compute and write all the error covariance normalization coefficients.
The normalization coefficients need to be computed only once for a particular application provided that the grid, land/sea masking (if any), and decorrelation scales (HdecayI, VdecayI, HdecayB, VdecayB, and HdecayF) remain the same. Notice that large spatial changes in the normalization coefficient structure are observed near the open boundaries and land/sea masking regions.
Instructions
To run this application you need to take the following steps:
- We need to run the model application for a period that is long enough to compute meaningful circulation statistics, like mean and standard deviations for all prognostic state variables (zeta, u, v, T, and S). The standard deviations are written to NetCDF files and are read by the 4D-Var algorithm to convert modeled error correlations to error covariances. We need the standard deviations for initial conditions, model error (weak constraint 4D-Var), open boundary conditions (ADJUST_BOUNDARY), and surface forcing (ADJUST_WSTRESS and ADJUST_STFLUX). If the balance operator is activated (BALANCE_OPERATOR and ZETA_ELLIPTIC), the standard deviations for the initial and model error are in terms of the unbalanced error covariance (K Bu KT). The balance operator imposes a multivariate constraint on the error covariance such that the unobserved variable information is extracted from observed data by establishing balance relationships (i.e., T-S empirical formulas, hydrostactic balance, and geostrophic balance) with other state variables (Weaver et al., 2005). The balance operator is not used in the tutorial.
The standard deviations for WC13 have already been created for you:
../Data/wc13_std_m.nc model error (weak constraint)
../Data/wc13_std_b.nc open boundary conditions
../Data/wc13_std_f.nc surface forcing (wind stress and net heat flux)
- Customize your preferred build script and provide the appropriate values for:
- Root directory, MY_ROOT_DIR
- ROMS source code, MY_ROMS_SRC
- Fortran compiler, FORT
- MPI flags, USE_MPI and USE_MPIF90
- Path of MPI, NetCDF, and ARPACK libraries according to the compiler are set in my_build_paths.csh. Notice that you need to provide the correct places of these libraries for your computer. If you want to ignore this section, set USE_MY_LIBS value to no.
- Notice that the most important CPP option for this application is specified in the build script instead of wc13.h:setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DNORMALIZATION"This is to allow flexibility with different CPP options.
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DADJUST_BOUNDARY"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DADJUST_STFLUX"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DADJUST_WSTRESS"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DANA_INITIAL"
setenv MY_CPP_FLAGS "${MY_CPP_FLAGS} -DANA_SPONGE"For this to work, however, any #undef directives MUST be avoided in the header file wc13.h since it has precedence during C-preprocessing. - You MUST use the build script to compile.
- Customize the ROMS input script roms_wc13.in and specify the appropriate values for the distributed-memory partition. It is set by default to:Notice that the adjoint-based algorithms can only be run in parallel using MPI. This is because of the way that the adjoint model is constructed.
- Customize the configuration script job_normalization.csh and provide the appropriate place for the substitute Perl script:set SUBSTITUTE=${ROMS_ROOT}/ROMS/Bin/substituteThis script is distributed with ROMS and it is found in the ROMS/Bin sub-directory. Alternatively, you can define ROMS_ROOT environmental variable in your .cshrc login script. For example, I have:setenv ROMS_ROOT /home/arango/ocean/toms/repository/trunk
- Execute the configuration job_normalization.csh before running the model. It copies the required files and creates the c4dvar.in input script from template s4dvar.in.
- Run ROMS with data assimilation:mpirun -np 8 romsM roms_wc13.in > & log &
Results
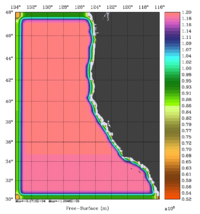
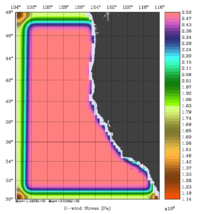
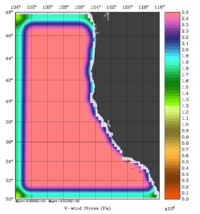
The error covariance normalization coefficients for free-surface, surface wind stress components, and surface net heat flux using the exact method are shown below:
 |
 |
 |
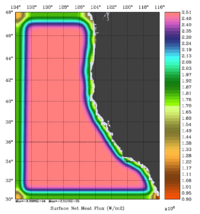 |
The error covariance normalization coefficients for 3D-momentum, temperature, and salinity at the surface using the exact method are shown below:
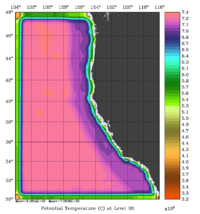 |
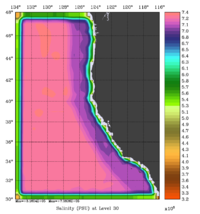 |
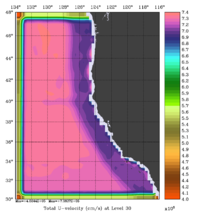 |
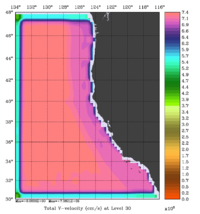 |
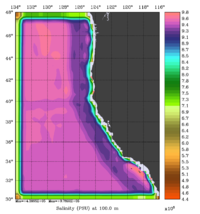
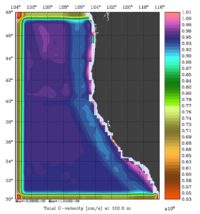
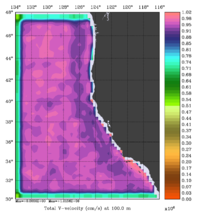
The error covariance normalization coefficients for 3D-momentum, temperature, and salinity at 100m using the exact method are shown below:
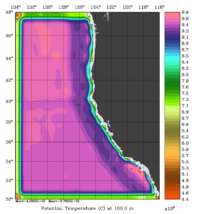 |
 |
 |
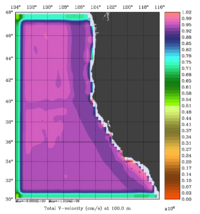 |
The error covariance normalization coefficients for free-surface, surface wind stress components, and surface net heat flux using the randomization method are shown below:
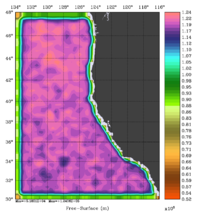 |
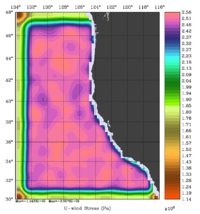 |
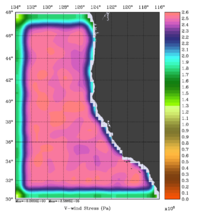 |
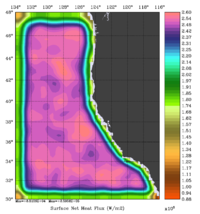 |
The error covariance normalization coefficients for 3D-momentum, temperature, and salinity at the surface using the randomization method are shown below:
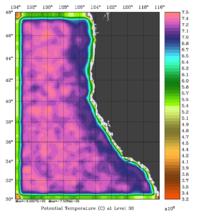 |
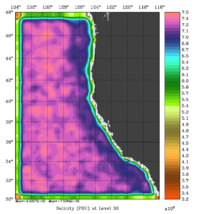 |
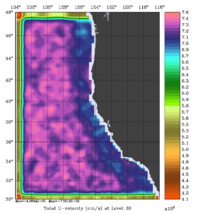 |
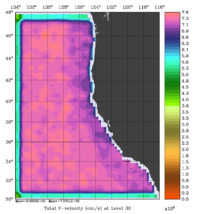 |
The error covariance normalization coefficients for 3D-momentum, temperature, and salinity at 100m using the randomization method are shown below:
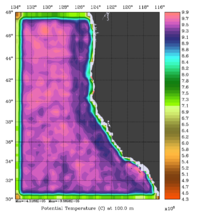 |
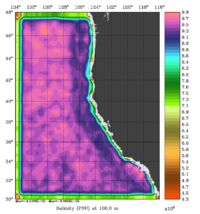 |
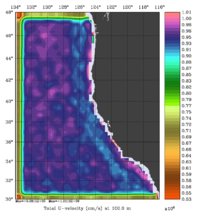 |
 |