ROMS/TOMS Developers

The incremental, strong contraint 4DVAR (IS4DVAR) approximated approach was proposed by Courtier et al. (1994) to reduce the computational cost and facilitate better preconditioning. We follow the algorithm proposed by Weaver et al (2002) that defines the increment to the difference from previous reference state.

Let x^k denote the state vector on the k-th outer loop such that δx^k is the increment difference from the previous state

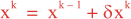
where x^{k -1} is the current estimate of the ocean state. It is equal to the background state for the first minimization (x⁰ = x_b, δx¹ = 0). The cost function on the k-th loop can be written as

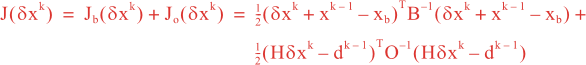
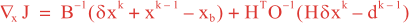
where d^{k – 1} = x_o – Hx^{k – 1} is the innovation vector, x_o is the observation vector, x_b is the background state, H is a linear approximation of the observation operator H, and B and O are the background and observation error covariance matrices. Let’s introduce a new minimization variable δv, such that:

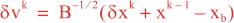
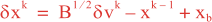
It is more convenient to work in terms of δv (minimization space: v-space). The conditioning of the J_b in v-space is optimal since it’s Hessian, ∂²J_b/∂v², yields the identity matrix. The gradient of J in v-space, denoted ∇_vJ, is given by:

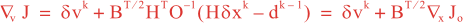
where B = B^T/2B^1/2 and B^T/2 denotes (B^1/2)^T, and ∇_xJ_o is the gradient of J_o in model space (x-space) which is computed using the adjoint model and given by:

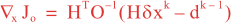
Following Weaver and Courtier (2001), the background-error covariance matrix can be factored as:

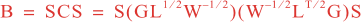
where S is a diagonal matrix of background-error standard deviations, C is a symetric matrix of background-error correlations which can be factorized as C = C^1/2C^T/2, G is the normalization matrix which ensures that the diagonal elements of C are equal to unity, L is a 3D self-adjoint filtering operator, and W is the grid cell area (2D fields) or volume (3D fields).