We have been working on the new conjugate gradient algorithms for IS4DVAR for awhile. A full description of the conjugate gradient algorithm is given in Fisher and Courtier (1995), ECMWF Tech Memo 220. Many thanks to Mike Fisher for providing us his prototype code and Andy Moore for adapting it to ROMS framework.
Currently we have two conjugate gradient algorithms: cgradient.h and cgradient_lanczos.h. The cgradient.h algorithm was decribed in previous post. The new alogorithm cgradient_lanczos.h is used when the LANCZOS CPP option is activated. This routine exploits the close connection between the conjugate gradient minimization and the Lanczos algorithm:
q(k) = g(k) / ||g(k)||
If we eliminate the descent directions (Eqs 5d and 5g) and multiply by the Hessian matrix, we get the Lanczos recurrence relationship:
H q(k+1) = γ(k+1) q(k+2) + δ(k+1) q(k+1) + γ(k) q(k)
with
δ(k+1) = (1 / α(k+1)) + (β(k+1) / α(k))
γ(k) = - SQRT ( β(k+1)) / α(k) )
since the gradient and Lanczos vectors are mutually orthogonal the recurrence maybe written in matrix form as:
H Q(k) = Q(k) T(k) + γ(k) q(k+1) e'(k)
with
{ q(1), q(2), q(3), ..., q(k) }
Q(k) = { . . . . }
{ . . . . }
{ . . . . }
{ δ(1) γ(1) }
{ γ(1) δ(2) γ(2) }
{ . . . }
T(k) = { . . . }
{ . . . }
{ γ(k-2) δ(k-1) γ(k-1) }
{ γ(k-1) δ(k) }
e'(k) = { 0, ...,0, 1 }
The eigenvalues of T(k) and the vectors formed by Q(k)*T(k) are approximations to the eigenvalues and eigenvectors of the Hessian. They can be used for preconditioning.
The tangent linear model conditions and associated adjoint in terms of the Lanzos algorithm are:
X(k) = X(0) + Q(k) Z(k) T(k) Z(k) = - transpose[Q(k0)] g(0) where k Inner loop iteration α(k) Conjugate gradient coefficient β(k) Conjugate gradient coefficient δ(k) Lanczos algorithm coefficient γ(k) Lanczos algorithm coefficient H Hessian matrix Q(k) Matrix of orthonormal Lanczos vectors T(k) Symmetric, tri-diagonal matrix Z(k) Eigenvectors of Q(k)*T(k) e'(k) Tansposed unit vector g(k) Gradient vectors (adjoint solution: GRAD(J)) q(k) Lanczos vectors <...> Dot product ||...|| Euclidean norm, ||g(k)|| = SQRT( <g(k),g(k)> )
The figures below show the cost function and gradient norm for a double gyre run with (solid) and without (solid and dots) preconditioning. Notice that the preconditioned cost function has smaller values. The big improvement, however, is in the gradient norm. These results show the same behavior as that described in Mike Fisher unpublished manuscript. So we conclude that the new conjugate gradient algorithms are working very well.
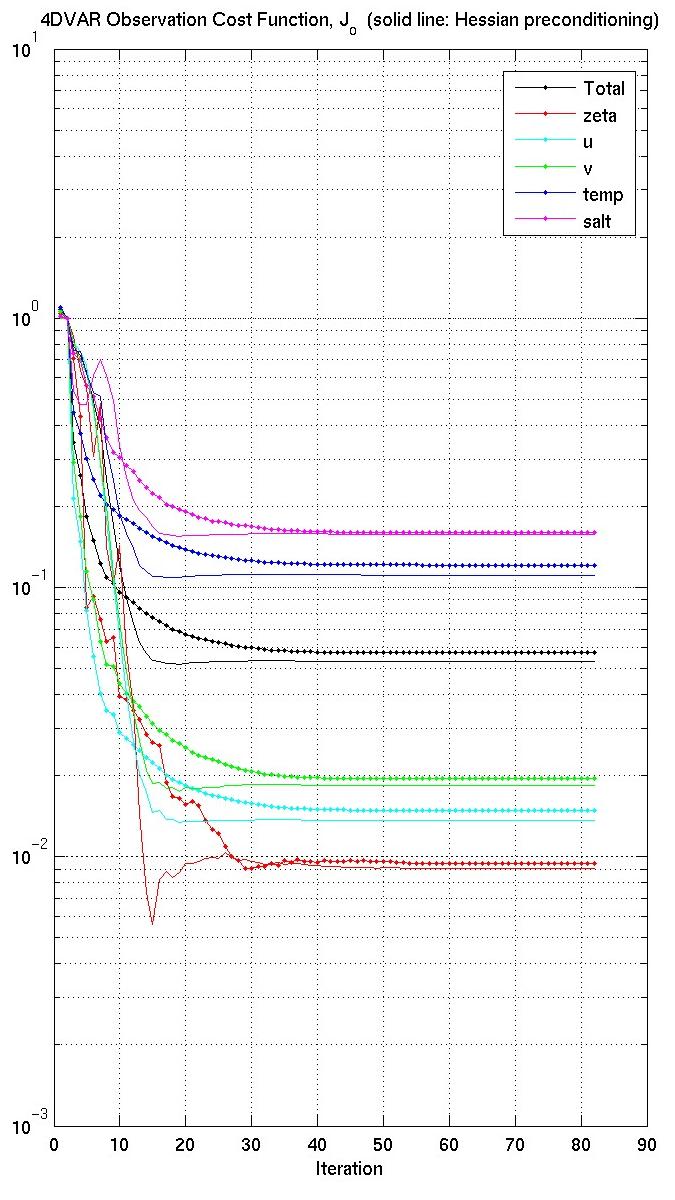
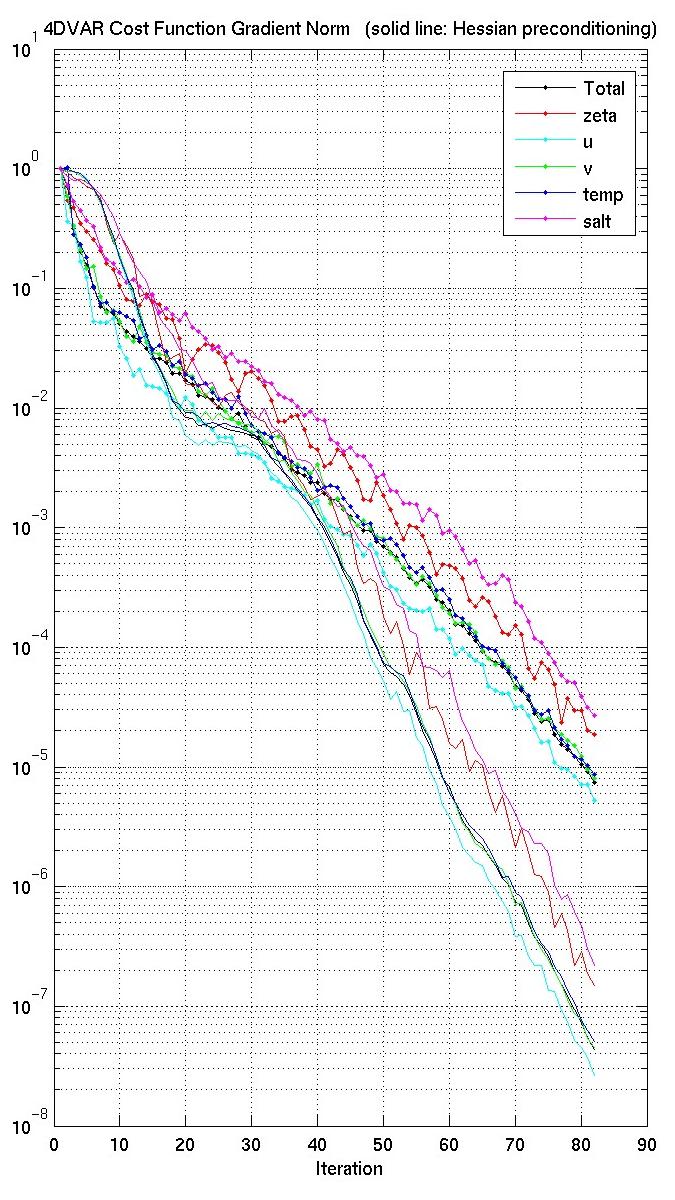
Therefore, the strategy is to run both algorithms for a particular application. If the observations are in the same locations, the Hessian eigenvectors need to be computed only once and saved into HSSname NetCDF file using the LANCZOS CPP option (cgradient_lanczos.h) and logical switch LhessianEV = .TRUE.. Then, these eigenvalues and eigenvectors can be read by the cgradient.h (LANCZOS off) with logical (Lprecond = .TRUE.) to approximate the Hessian during preconditioning. We prefer the cgradient.h algorithm because we can compute the value of the cost function at each inner loop iteration. In the Lanczos algorithm (cgradient_lanczos.h) we only know the value of the cost function at the last inner loop. Notice that both algorithm (not shown) give very similar solutions.