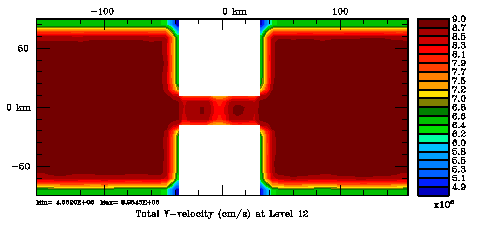
In 4DVAR the background/model error covariance is modeled using a generalized diffusion operator. We use the approach of Weaver and Courtier (2001) to compute the correlation statistics. The normalization matrix is used to convert the covariance matrix into a correlation matrix. It insures that the diagonal elements of the background/model error covariance are equal to unity. The normalization matrix is spatially dependent and affected by the land/sea masking. Currently, there are two methods to compute these coefficients: exact (Nmethod=0) and randomization (Nmethod=1). The exact method is very expensive since the normalization coefficients are computed by perturbing each model grid cell with a delta function scaled by the area (2D) or volume (3D), and then convolving with the squared-root adjoint and tangent linear diffusion operators (ad_conv_2d.F, ad_conv_3d.F, tl_conv_2d.F, tl_conv_3d.F). The randomization (approximated) method is cheaper (Fisher and Courtier, 1995). The coefficients are initialized with random numbers having a uniform distribution (drawn from a normal distribution with zero mean and unit variance). Then, scaled by the inverse, squared-root cell area (2D) or volume (3D) and convolved with squared-root tangent linear diffusion operator. These normalization coefficients are computed in Utility/normalization.F. The correlation parameters are specified, for each state variable, in s4dvar.in. The horizontal and vertical decorrelation scales are Hdecay(:) and Vdecay(:), respectively. Check 4DVAR input script for more details. In realistic applications, it is highly recomended to do the vertical convolutions implicitly (IMPLICIT_VCONV). Otherwise, it will take too many iterations since the very different horizontal and vertical length scales.
Several plots are shown below for the normalization coefficients in the CHANNEL_NECK application. We are using a 10 km horizontal decorrelation scale and 10 m vertical decorrelation scale. This application is east-west periodic and has land/sea masking in the constriction. The normalization coefficents were computed using both exact and randomization methods. The number of iterations in the randomization method is set to Nrandom=50000 to achieve a statistical meaninfull population with approximately zero expectation mean and unit variance.
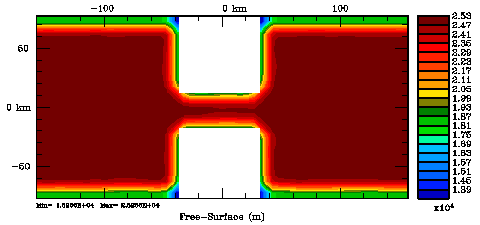
Normalization coefficients, 2D variable at RHO-points: Exact Method
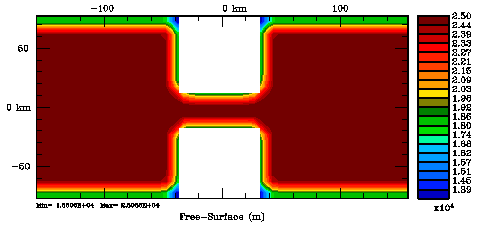
Normalization coefficients, 2D variable at RHO-points: Randomization Method
Normalization coefficients, 2D variable at U-points: Exact Method
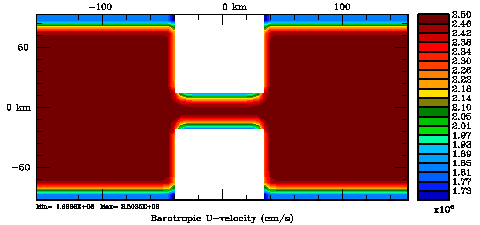
Normalization coefficients, 2D variable at U-points: Randomization Method
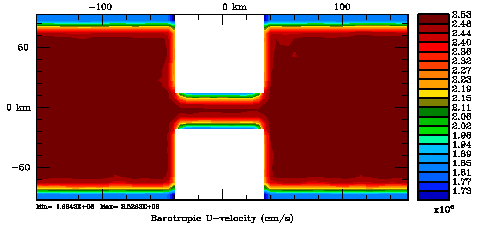
Normalization coefficients, 2D variable at V-points: Exact Method
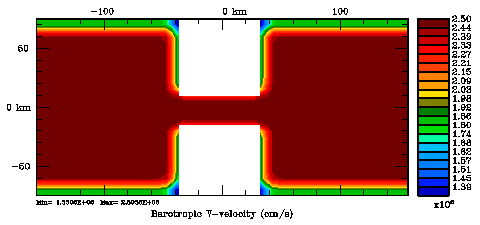
Normalization coefficients, 2D variable at V-points: Randomization Method
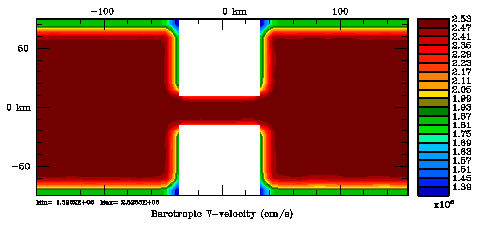
Normalization coefficients, 3D variable at RHO-points, surface level: Exact Method
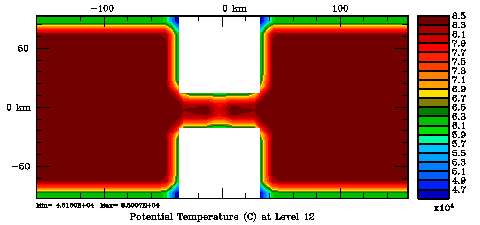
Normalization coefficients, 3D variable at RHO-points, surface level: Randomization Method
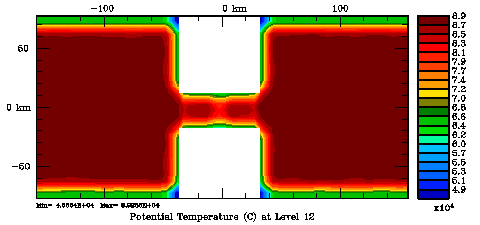
Normalization coefficients, 3D variable at U-points, surface level: Exact Method
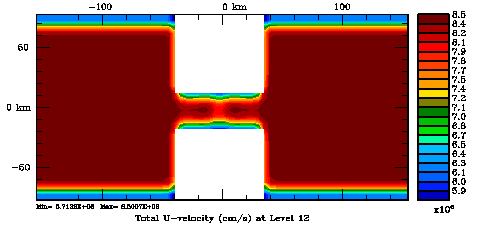
Normalization coefficients, 3D variable at U-points, surface level: Randomization Method
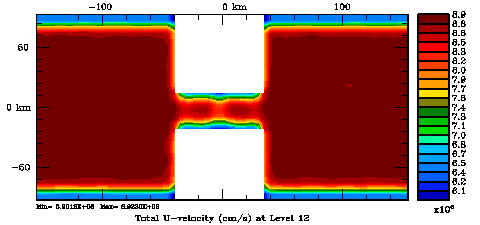
Normalization coefficients, 3D variable at V-points, surface level: Exact Method
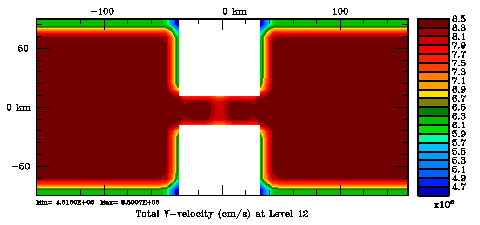
Normalization coefficients, 3D variable at V-points, surface level: Randomization Method