Added a new incremental, strong contraint 4DVAR driver which uses the conjugate gradient algorithm proposed by Mike Fisher (ECMWF). Many thanks to Mike for providing us his unpublished manuscript (Efficient Minimization of Quadratic Penalty Functions, 1997) and prototype source code. Many thanks to Andy Moore for his help in the debugging of the new algorithm.
The new driver is more efficient since only one call to the tangent linear model is needed per inner loop iteration. The old algorithm required a second call to compute the optimum conjugate gradient algorithm step size. The new algorithm can be activated with cpp option IS4DVAR and the old with IS4DVAR_OLD.
The developing of this new driver has been done in two stages:
- Basic conjugate gradient algorithm where the new initial conditions increment and its associated gradient are adjusted to the optimum line search. In addition, the new gradient at each inner loop iteration is orthogonalized against all previous gradient using the modified Gramm-Schmidt algorithm.
- Lanczos algorithm to compute the eigenvectors and eigenvalues used to estimate the minimization Hessian matrix for preconditioning.
Currently, only the first stage is available. The new conjugate gradient cgradient.F follows Fisher (1997) algorithm:
Given an initial increment X(0), gradient G(0), descent direction d(0)=-G(0), and trial step size τ(0) , the minimization algorithm at the k-iteration is:
- Run tangent linear model initialized with trial step, Xhat(k), Eq 5a:
Xhat(k) = X(k) + tau(k) * d(k)
- Run adjoint model to compute gradient at trial point, Ghat(k), Eq 5b:
Ghat(k) = GRAD[ f(Xhat(k)) ]
- Compute optimum step size, α(k), Eq 5c:
α(k) = τ(k) * <d(k),G(k)> / (<d(k),G(k)> – <d(k),Ghat(k)>)
here <…> denotes dot product.
- Compute new starting point (TLM increments), X(k+1), Eq 5d:
X(k+1) = X(k) + α(k) * d(k)
- Compute gradient at new point, G(k+1), Eq 5e:
G(k+1) = G(k) + (alpha(k) / tau(k)) * (Ghat(k) – G(k))
- Orthogonalize new gradient, G(k+1), against all previous gradients [G(k), …, G(0)], in reverse order, using the modified Gramm-Schmidt algorithm. Notice that we need to save all inner loop gradient solutions. Currently, all the gradients are stored in the adjoint NetCDF file(s) and not in memory.
- Compute new descent direction, d(k+1), Eqs 5g and 5f:
β(k+1) = <G(k+1),G(k+1)> / <G(k),G(k)>
d(k+1) = – G(k+1) + β(k+1) * d(k)
After the first iteration, the trial step size is:
τ(k) = α(k-1)
The new driver is is4dvar_ocean.h and the old becomes is4dvar_ocean_old.h. The old driver is kept for comparison and will become obsolete in the future. A new generic dot product routine state_dotprod.F is introduced.
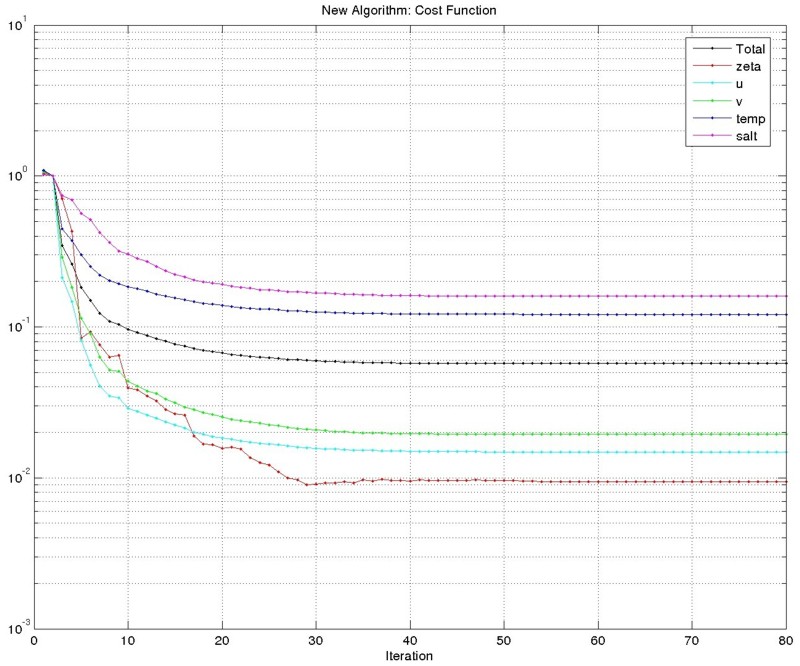
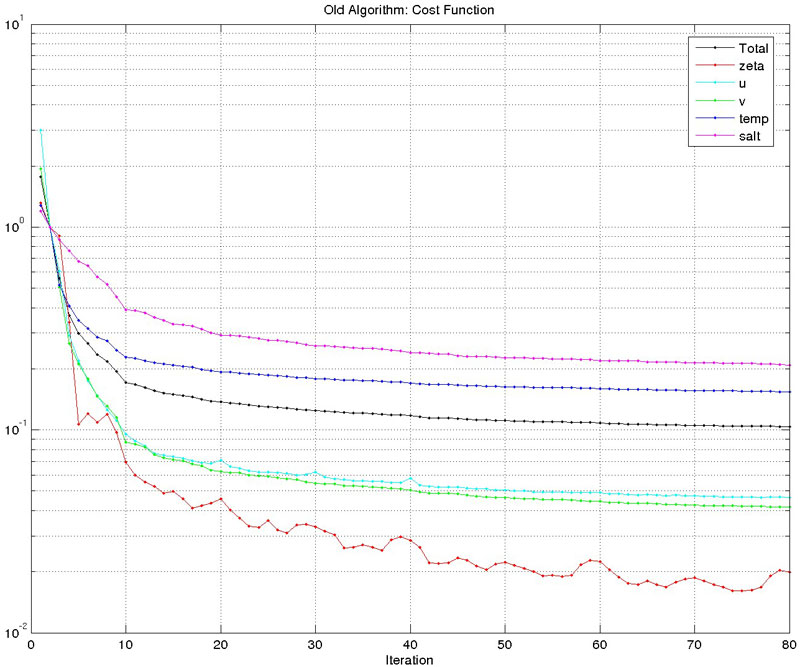
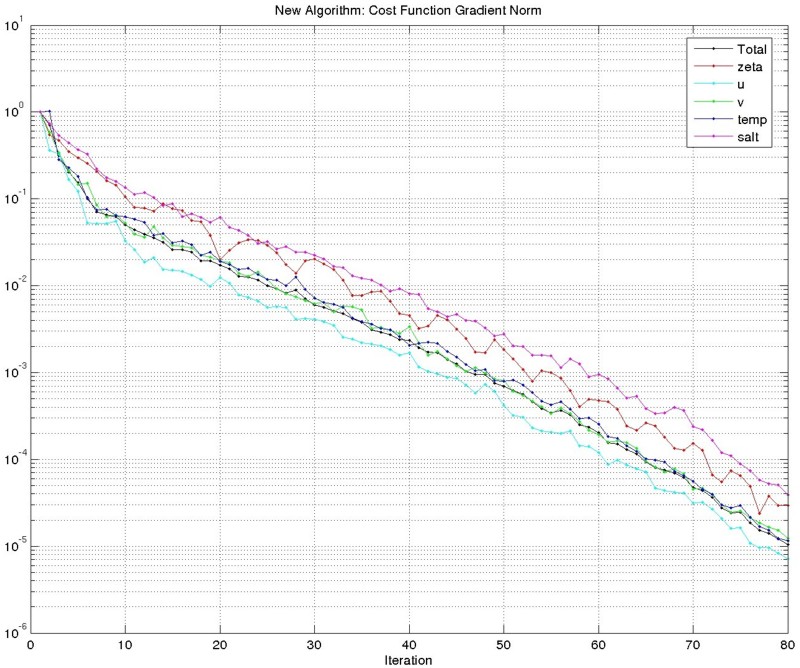
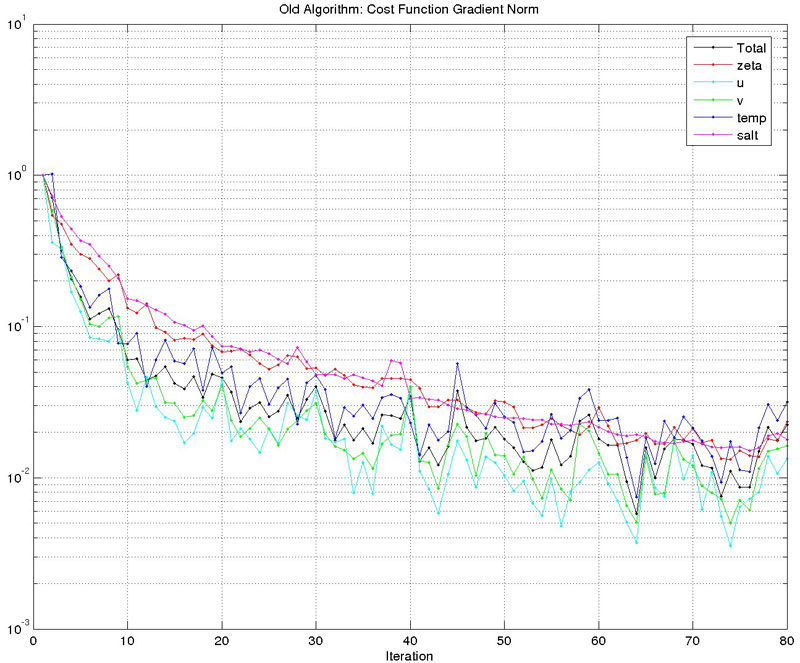
The new algorithm is still under testing but the results are promising as shown below for the double gyre test case (outer=1, inner=80 for both new and old drivers). Notice that the gradient norm in the new algorithm decreased by about five-orders of magnitude compared to only two-orders of magnitude in the old algorithm. The new algorithm is much cheaper.
The minimization of the cost function is also improved.