Numerical Solution Technique
Horizontal Discretization
<wikitex> In the horizontal, the ROMS governing equations are discretized over a boundary-fitted, orthogonal curvilinear coordinates ($\xi$, $\eta$) grid. The general formulation of the curvilinear coordinates system allows Cartesian, polar and spherical coordinates applications. The transformation of any of these coordinates to ROMS ($\xi$, $\eta$) grid is specified in the metric terms (pm, pn).
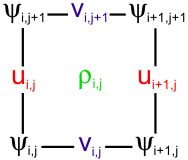
The model state variables are staggered using an Arakawa C-grid. As illustrated below, the free-surface (zeta), density (rho), and active/passive tracers (t) are located at the center of the cell whereas the horizontal velocity (u and v) are located at the west/east and south/north edges of the cell, respectively. That is, the density is evaluated between points where the currents are evaluated.
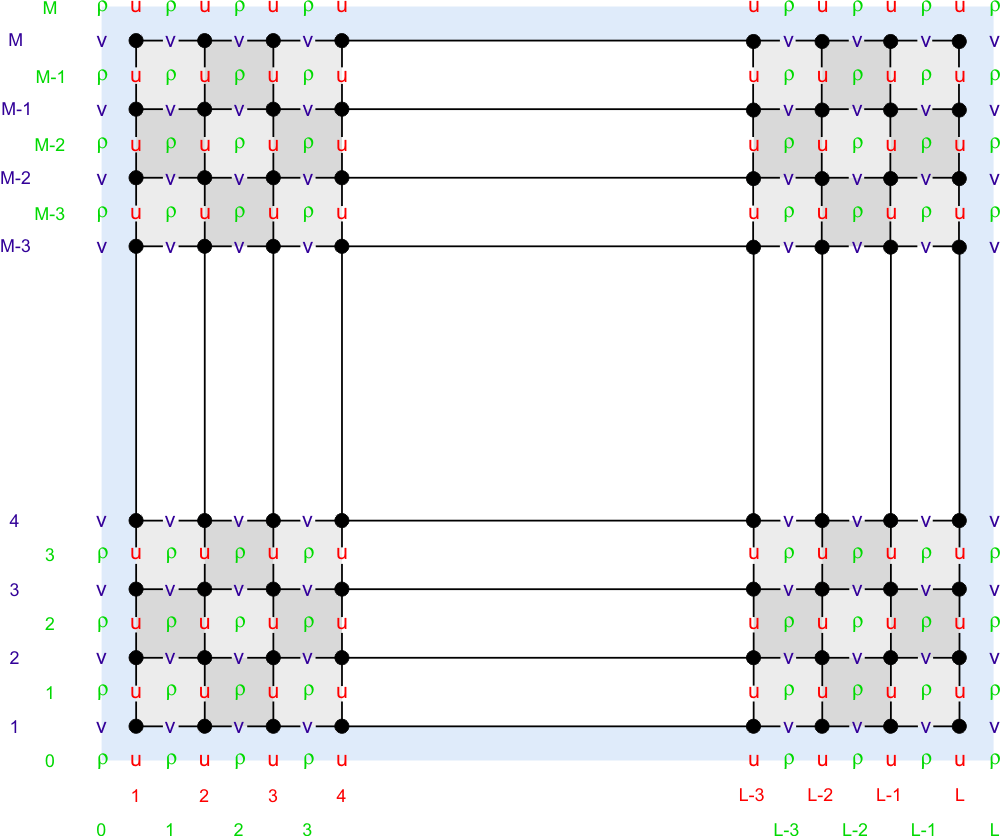
In ROMS all the state arrays are dimensioned the same size to facilitate parallelization. However, the computational ranges for all the state variables are:
| Variable | Interior Range | Full Range |
|---|---|---|
| $\rho$-type | 1:Lm(ng),1:Mm(ng) | 0:L(ng),0:M(ng) |
| $\psi$-type | 2:Lm(ng),2:Mm(ng) | 1:L(ng),1:M(ng) |
| u-type | 2:Lm(ng),1:Mm(ng) | 1:L(ng),0:M(ng) |
| v-type | 1:Lm(ng),2:Mm(ng) | 0:L(ng),1:M(ng) |
</wikitex>
Coastal boundaries can also be specified as a finite-discretized grid via land/sea masking arrays (rmask, umask, and vmask).
Vertical Discretization
<wikitex> The ROMS governing equations are discretized over variable topography using a stretched, terrain-following, vertical coordinate. As a result, each grid cell may have different level thickness (Hz) and volume. The model state variables are vertically staggered so that horizontal momentum (u, v), (rho), and active/passive tracers (t) are located at the center of the grid cell. The vertical velocity (omega, w) and vertical mixing variables (Akt, Akv, etc) are located at the bottom and top faces of cell. See diagram below.
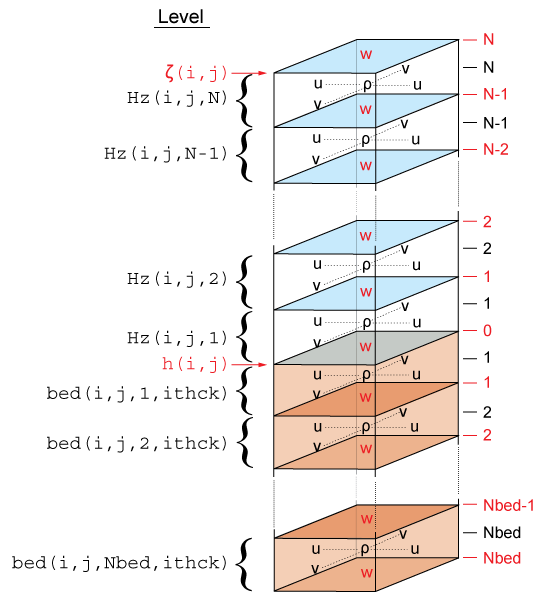
The total thickness of the water column is $\zeta(i,j)+h(i,j)$. The bathymetry (h) is usually time invariant whereas the free-surface (zeta) evolves in time. However, in sediment applications h changes with time when SED_MORPH is activated. At input and output, the bathymetry is always a positive quantity. However, the depths z_r(i,j,k) and z_w(i,j,k) are negative for all locations below the mean sea level.
</wikitex>
Masking of Land Areas
<wikitex>
ROMS has the ability to work with interior land areas, although the
computations occur over the entire model domain. The grid structure as a whole is shown above while two land cells are shown here:
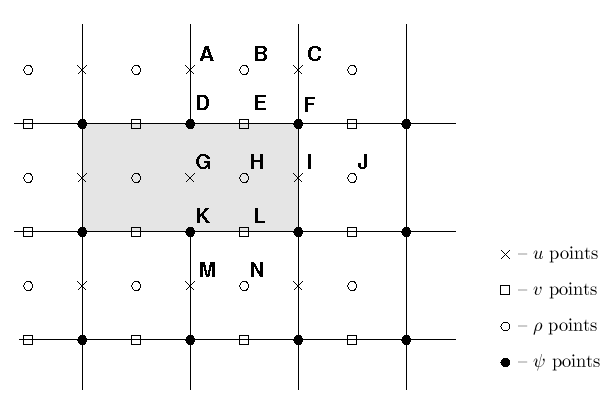
The process of defining which areas are to be masked happens during the preparation of the grid file, while this section describes how the masking affects the computation of the various terms in the equations of motion. </wikitex>
Velocity points
<wikitex> At the end of every timestep, the values of many variables within the masked region are set to zero by multiplying by the mask for either the $u$, $v$ or $\rho$ points. This is appropriate for the $v$ points E and L in the figure, since the flow in and out of the land should be zero. It is likewise appropriate for the $u$ point at I, but is not necessarily correct for point G. The only term in the $u$ equation that requires the $u$ value at point G is the horizontal viscosity, which has a term of the form ${\partial \over \partial \eta} \nu {\partial u \over \partial \eta}$. Since point G is used in this term by both points A and M, it is not sufficient to replace its value with that of the image point for A. Instead, the term ${\partial u \over \partial \eta}$ is computed and the values at points D and K are replaced with the values appropriate for either free-slip or no-slip boundary conditions. Likewise, the term ${\partial \over \partial \xi} \nu {\partial v \over \partial \xi}$ in the $v$ equation must be corrected at the mask boundaries.
This is accomplished by having a fourth mask array defined at the $\psi$ points, in which the values are set to be no-slip in metrics.F. For no-slip boundaries, we count on the values inside the land (point G) having been zeroed out. For point D, the image point at G should contain minus the value of $u$ at point A. The desired value of ${\partial u \over \partial \eta}$ is therefore $2 u_{\bf A}$ while instead we have simply $u_{\bf A}$. In order to achieve the correct result, we multiply by a mask which contains the value 2 at point D. It also contains a 2 at point K so that ${\partial u \over \partial \eta}$ there will acquire the desired value of $-2 u_{\bf M}$. The corner point F is set to have a value of 1. </wikitex>
Temperature, Salinity and Surface Elevation
<wikitex> The handling of masks by the temperature, salinity and surface elevation equations is similar to that in the momentum equations, and is in fact simpler. Values of $T$, $S$ and $\zeta$ inside the land masks, such as point H in the figure above, are set to zero after every timestep. This point would be used by the horizontal diffusion term for points B, J, and N. This is handled by setting the first derivative terms at points E, I, and L to zero, to be consistent with a no-flux boundary condition. Note that the equation of state must be able to handle $T = S = 0$ since this is the value inside masked regions. </wikitex>
Nesting Grids
<wikitex> ROMS has a nested design structure for the temporal coupling between a hierarchy of parent and child grids. All the state model variables are dynamically allocated and passed as arguments to the computational routines via Fortran-90 dereferenced pointer structures. All private arrays are automatic; their size is determined when the procedure is entered. This code structure facilitates computations over nested grids of different topologies. There are three types of nesting capabilities in ROMS:
- Refinement Grids which provide increased resolution (3:1 or 5:1) in a specific region,
- Mosaics Grids which connect several grids along their edges, and
- Composite Grids which allow overlap regions of aligned and non-aligned grids.
</wikitex>
Refinement Grids
<wikitex>
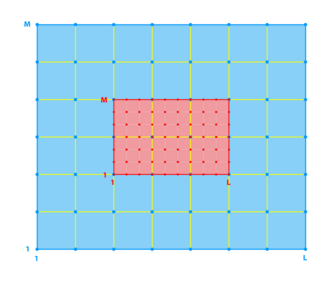
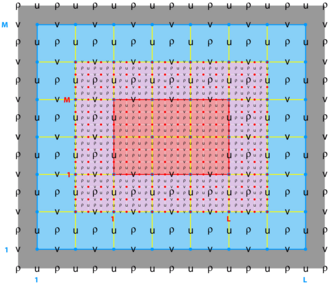
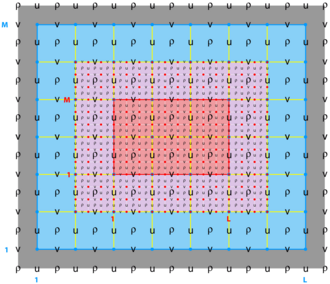
</wikitex>
Mosaic Grids
<wikitex>
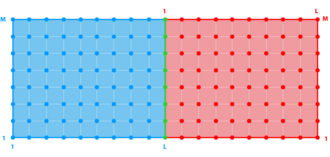
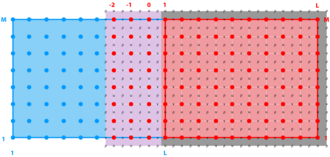
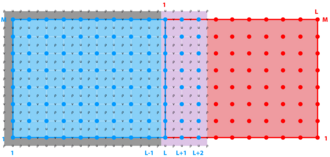
</wikitex>
Composite Grids
<wikitex>
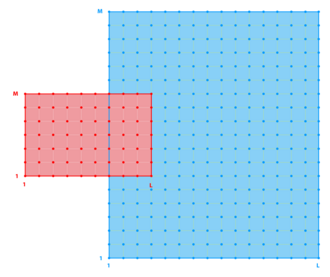
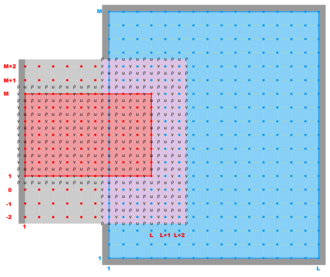
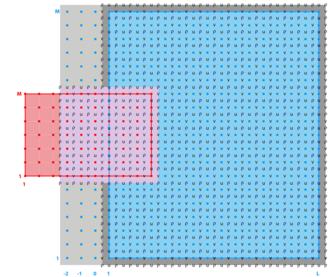
</wikitex>
Conservation Properties
<wikitex> ROMS conserves the first moments of $u, v, S,$ and $T$. This is accomplished by using the flux form of the momentum and tracer equations. It is also necessary to be careful when averaging between the velocity and tracer grids, for instance to obtain $u$ at $\rho$ points. The semi-discrete form of the dynamic equations for second-order finite differences would be: $$ \frac{\partial}{\partial t} \left(\frac{u\overline{H_z}^\xi}
{\overline{m}^\xi\overline{n}^\xi} \right) +
\delta_{\xi} \left\{ \overline{u}^{\xi}
\overline{\left( \frac{u \overline{H_z}^{\xi}}{\overline{n}^{\xi}}
\right)}^{\xi}
\right\} + \delta_{\eta} \left\{ \overline{u}^{\eta}
\overline{\left( \frac{v \overline{H_z}^{\eta}}{\overline{m}^{\eta}}
\right) }^{\xi} \right\}
+ \delta_s \left\{ \overline{u}^s \overline{ \left(
{H_z \Omega \over m n} \right) }^\xi \right\}$$
$$ - \overline{ \left\{
{f \over m n}
+ \overline{v}^{\eta} \,
\delta_{\xi} \left( \frac{1}{n} \right) -
\overline{u}^{\xi} \,
\delta_{\eta} \left( \frac{1}{m} \right)
\right\} H_z \overline{v}^{\eta} }^{\xi} =$$
$$ - \frac{\overline{H_z}^{\xi}}{\overline{n}^{\xi}}\delta_{\xi}\phi
- {g \overline{H_z}^{\xi} \over \rho_o \overline{n}^{\xi}}
\overline{\rho}^{\xi} \delta_{\xi} z
- {g \overline{H_z}^{\xi} \over \rho_o \overline{n}^{\xi}}
( \rho_o + \overline{\rho}^{\xi} ) \delta_{\xi} \zeta +$$
$$
{ 1 \over \overline{m}^{\xi}\overline{n}^{\xi}} {\partial \over
\partial s} \left( {\overline{K_m}^{\xi} \over
\overline{\Delta z}^{\xi}} {\partial u
\over \partial s} \right) +
{\cal D}_u + {\cal F}_u$$
$$ \frac{\partial}{\partial t} \left(\frac{v\overline{H_z}^\eta}
{\overline{m}^\eta\overline{n}^\eta} \right) +
\delta_{\xi} \left\{ \overline{v}^{\xi}
\overline{\left( \frac{u \overline{H_z}^{\xi}}{\overline{n}^{\xi}}
\right)}^{\eta}
\right\} + \delta_{\eta} \left\{ \overline{v}^{\eta}
\overline{\left( \frac{v \overline{H_z}^{\eta}}{\overline{m}^{\eta}}
\right) }^{\eta}\right\}
+ \delta_s \left\{ \overline{v}^s \overline{ \left(
{H_z \Omega \over m n} \right) }^\eta \right\}$$
$$ + \overline{ \left\{
{f \over m n}
+ \overline{v}^{\eta} \,
\delta_{\xi} \left( \frac{1}{n} \right) -
\overline{u}^{\xi} \,
\delta_{\eta} \left( \frac{1}{m} \right)
\right\} H_z \overline{u}^{\xi} }^{\eta} =$$
$$ - {\overline{H_z}^{\eta} \over \overline{m}^{\eta}}\delta_{\eta}\phi
- {g \overline{H_z}^{\eta} \over \rho_o \overline{m}^{\eta}}
\overline{\rho}^{\eta} \delta_{\eta} z
- {g \overline{H_z}^{\eta} \over \rho_o \overline{m}^{\eta}}
( \rho_o + \overline{\rho}^{\eta} ) \delta_{\eta} \zeta +$$
$$ { 1 \over \overline{m}^{\eta}\overline{n}^{\eta}} {\partial \over
\partial s} \left( {\overline{K_m}^{\eta} \over
\overline{\Delta z}^{\eta}} {\partial v
\over \partial s} \right) +
{\cal D}_v + {\cal F}_v$$
$$ {\partial \over \partial t} \left( {H_z C \over m n} \right)
+ \delta_{\xi} \left( {u \overline{H_z}^\xi \overline{C}^\xi
\over \overline{n}^\xi} \right)
+ \delta_{\eta} \left( {v \overline{H_z}^\eta \overline{C}^\eta
\over \overline{m}^\eta} \right)
+ \delta_s \left( \overline{C}^s
{H_z \Omega \over m n} \right) =$$
$$ { 1 \over mn} {\partial \over
\partial s} \left( {K_m \over
\Delta z} {\partial C
\over \partial s} \right) +
{\cal D}_C + {\cal F}_C$$
$$ \rho = \rho(S,T,P)$$
$$\phi(s) = - {g \over \rho_o} I_{s}^{0} H_z \rho$$
Here $\delta_{\xi}$, $\delta_{\eta}$ and $\delta_s$ denote simple centered finite-difference approximations to $\partial / \partial \xi$, $\partial / \partial \eta$ and $\partial / \partial s$ with the differences taken over the distances $\Delta\xi$, $\Delta\eta$ and $\Delta s$, respectively. $\Delta z$ is the vertical distance from one $\rho$ point to another. $\overline{ ( \qquad )}^{\xi}$, $\overline{ ( \qquad )}^{\eta}$ and $\overline{ ( \qquad)}^s$ represent averages taken over the distances $\Delta\xi$, $\Delta \eta$ and $\Delta_s$. $I_s^0$ indicates a second-order vertical integral computed as a sum from level $s$ to the surface at $s=0$.
This method of averaging was chosen because it internally conserves first moments in the model domain, although it is still possible to exchange mass and energy through the open boundaries. The method is similar to that used in Arakawa and Lamb; however, their scheme also conserves enstrophy.
Note that this isn't exactly what ROMS is doing since ROMS now has a variety of options for the advection operators, it has a more complex timestep, and the vertical operations are done implicitly, with or without splines. These choices and the continuity equation will be discussed below. </wikitex>
Time-Stepping
<wikitex></wikitex>
Horizontal and Vertical Advection
<wikitex></wikitex>
Pressure Gradient
<wikitex></wikitex>