Numerical Solution Technique
Horizontal Discretization
In the horizontal, the ROMS governing equations are discretized over a boundary-fitted, orthogonal curvilinear coordinates (, ) grid. The general formulation of the curvilinear coordinates system allows Cartesian, polar and spherical coordinates applications. The transformation of any of these coordinates to ROMS (, ) grid is specified in the metric terms (pm, pn).
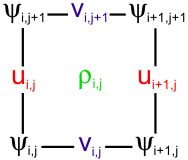
The model state variables are staggered using an Arakawa C-grid. As illustrated below, the free-surface (zeta), density (rho), and active/passive tracers (t) are located at the center of the cell whereas the horizontal velocity (u and v) are located at the west/east and south/north edges of the cell, respectively. That is, the density is evaluated between points where the currents are evaluated.
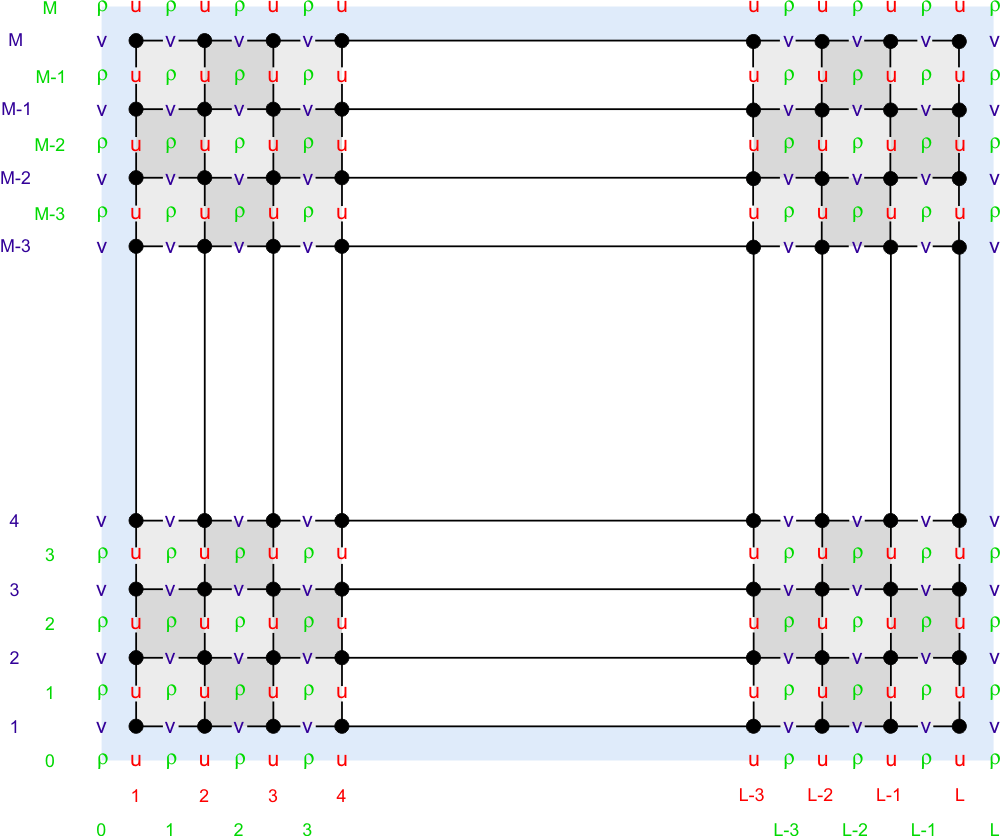
In ROMS all the state arrays are dimensioned the same size to facilitate parallelization. However, the computational ranges for all the state variables are:
| Variable | Interior Range | Full Range |
|---|---|---|
| -type | 1:Lm(ng),1:Mm(ng) | 0:L(ng),0:M(ng) |
| -type | 2:Lm(ng),2:Mm(ng) | 1:L(ng),1:M(ng) |
| u-type | 2:Lm(ng),1:Mm(ng) | 1:L(ng),0:M(ng) |
| v-type | 1:Lm(ng),2:Mm(ng) | 0:L(ng),1:M(ng) |
Coastal boundaries can also be specified as a finite-discretized grid via land/sea masking arrays (rmask, umask, and vmask).
Vertical Discretization
The ROMS governing equations are discretized over variable topography using a stretched, terrain-following, vertical coordinate. As a result, each grid cell may have different level thickness (Hz) and volume. The model state variables are vertically staggered so that horizontal momentum (u, v), (rho), and active/passive tracers (t) are located at the center of the grid cell. The vertical velocity (omega, w) and vertical mixing variables (Akt, Akv, etc) are located at the bottom and top faces of cell. See diagram below.
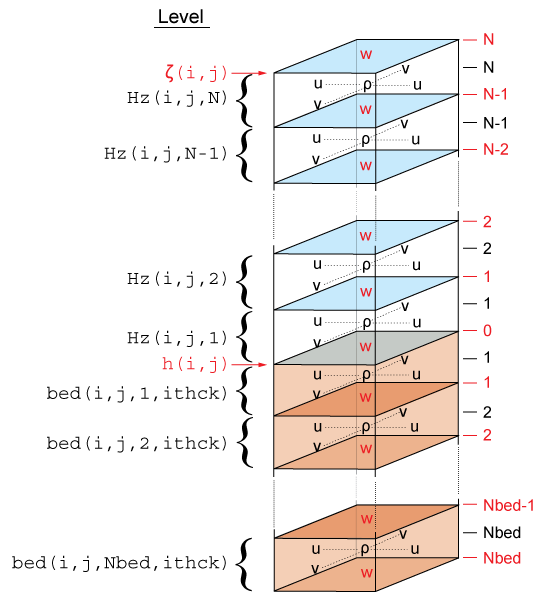
The total thickness of the water column is . The bathymetry (h) is usually time invariant whereas the free-surface (zeta) evolves in time. However, in sediment applications h changes with time when SED_MORPH is activated. At input and output, the bathymetry is always a positive quantity. However, the depths z_r(i,j,k) and z_w(i,j,k) are negative for all locations below the mean sea level.
Masking of Land Areas
ROMS has the ability to work with interior land areas, although the computations occur over the entire model domain. The grid structure as a whole is shown above while two land cells are shown here:
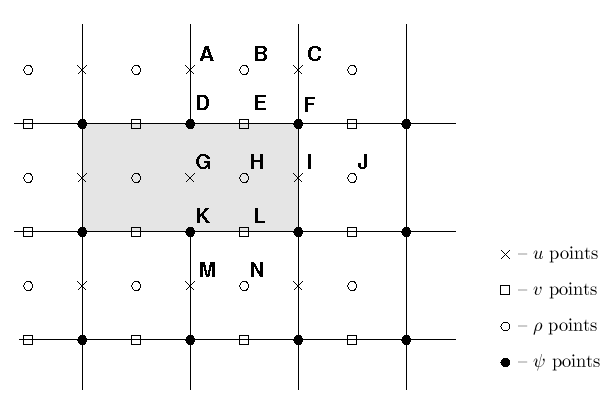
The process of defining which areas are to be masked happens during the preparation of the grid file, while this section describes how the masking affects the computation of the various terms in the equations of motion.
Velocity points
At the end of every timestep, the values of many variables within the masked region are set to zero by multiplying by the mask for either the , or points. This is appropriate for the points E and L in the figure, since the flow in and out of the land should be zero. It is likewise appropriate for the point at I, but is not necessarily correct for point G. The only term in the equation that requires the value at point G is the horizontal viscosity, which has a term of the form . Since point G is used in this term by both points A and M, it is not sufficient to replace its value with that of the image point for A. Instead, the term is computed and the values at points D and K are replaced with the values appropriate for either free-slip or no-slip boundary conditions. Likewise, the term in the equation must be corrected at the mask boundaries.
This is accomplished by having a fourth mask array defined at the points, in which the values are set to be no-slip in metrics.F. For no-slip boundaries, we count on the values inside the land (point G) having been zeroed out. For point D, the image point at G should contain minus the value of at point A. The desired value of is therefore while instead we have simply . In order to achieve the correct result, we multiply by a mask which contains the value 2 at point D. It also contains a 2 at point K so that there will acquire the desired value of . The corner point F is set to have a value of 1.
Temperature, Salinity and Surface Elevation
The handling of masks by the temperature, salinity and surface elevation equations is similar to that in the momentum equations, and is in fact simpler. Values of , and inside the land masks, such as point H in the figure above, are set to zero after every timestep. This point would be used by the horizontal diffusion term for points B, J, and N. This is handled by setting the first derivative terms at points E, I, and L to zero, to be consistent with a no-flux boundary condition. Note that the equation of state must be able to handle since this is the value inside masked regions.
Wetting and Drying
There is now an option to have wetting and drying in the model, in which a cell can switch between being wet or being dry as the tides come in and go out, for instance. Cells which are masked out as above are never allowed to be wet, however.
- In the case of wetting and drying, a critical depth, , is supplied by the user.
- The total water depth () is compared to . If the water level is less than this depth, no flux is allowed out of that cell. Water can always flow in and resubmerge the cell.
- The wetting and drying only happens during the 2-D computations; the 3-D computations see a depth of in the "dry" areas.
Time-Stepping Overview
While time-stepping the model, we have a stored history of the model fields at time , an estimate of the fields at the current time , and we need to come up with an estimate for time . For reasons of efficiency, we choose to use a split-explicit time-step, integrating the depth-integrated equations with a shorter time-step than the full 3-D equations. There is an integer ratio between the time-steps. The exact details of how the time-stepping is done vary from one version of ROMS to the next, with the east coast ROMS described here being older than other branches. Still, most versions have these steps:
- Take a predictor step for at least the 3-D tracers to time .
- Compute and for use in the depth-integrated time-steps, from the density either at time or time .
- Depth integrate the 3-D momentum right-hand side terms at time for use in the depth-integrated time-steps (or extrapolate to obtain an estimate of those terms).
- Take all the depth-integrated steps. Store weighted time-means of the , fields centered at both time and time (plus at time ). The latter requires this time-stepping to extend past time , using steps rather than just .
- Use the weighted time-means from depth-integrated fields to complete the corrector step for the 3-D fields to time .
Great care is taken to avoid the introduction of a mode-splitting instability due to the use of shorter time steps for the depth-integrated computations.
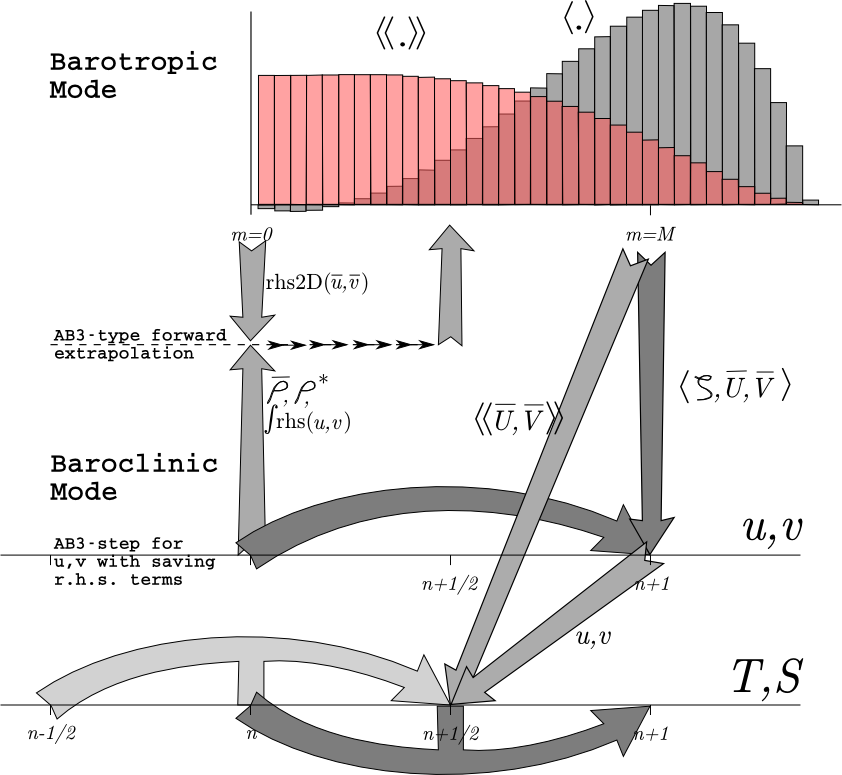
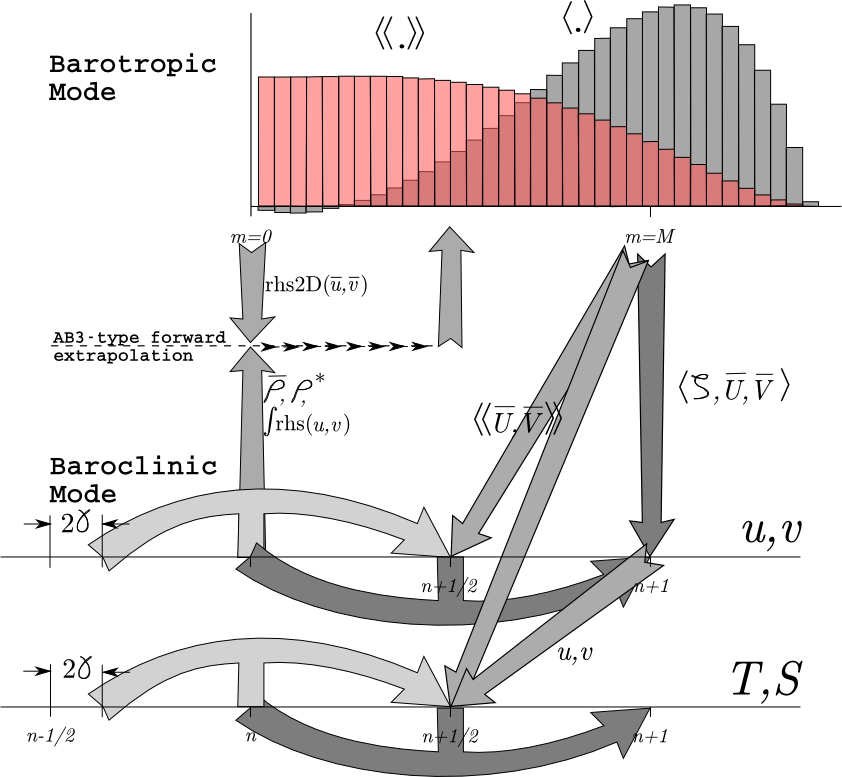
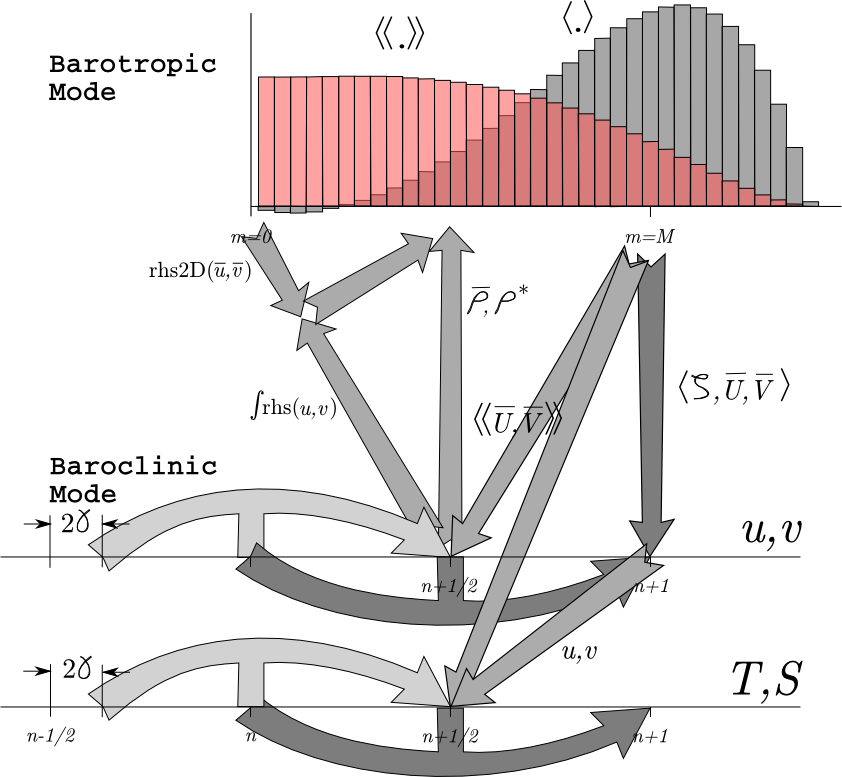
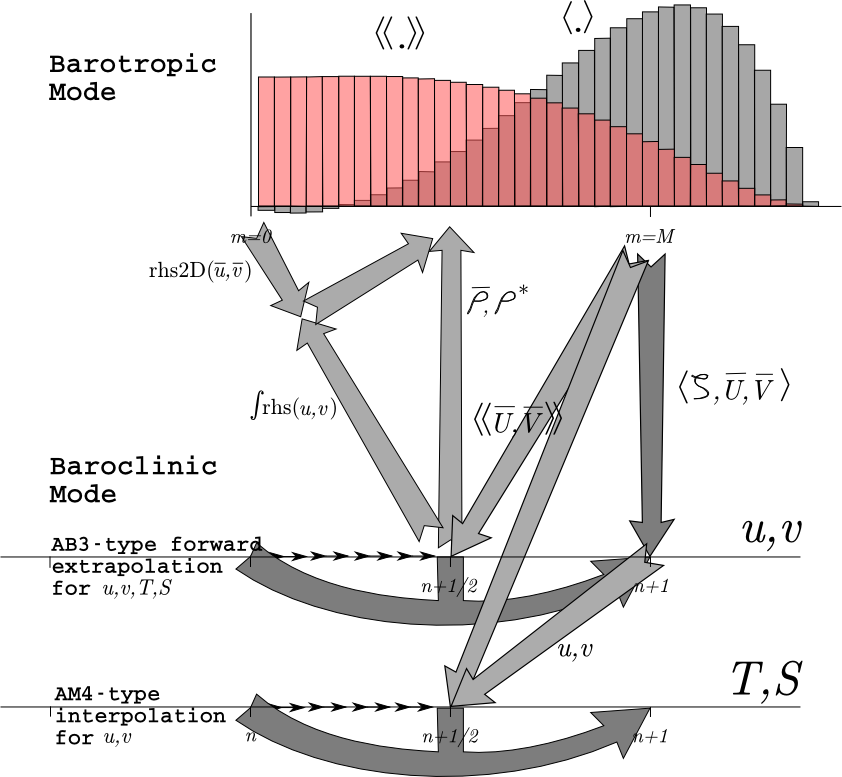
The mode coupling has evolved through the various ROMS versions, as shown in the figures below [from Shchepetkin and McWilliams (2008a)]. The time-stepping schemes are also listed in the following table and described in detail in Shchepetkin and McWilliams (2005) and Shchepetkin and McWilliams (2009); the relevant ones are described in Time-stepping Schemes Review.
The following figures show the time-stepping and mode coupling used in the various ROMS versions. In all, the curved arrows update the 3-D fields; those with "pillars" are leapfrog in nature with the pillar representing the r.h.s. terms. Straight arrows indicate exchange between the barotropic and baroclinic modes. The shape functions for the fast time steps show just one option out of many possibilities. The grey function has weights to produce an estimate at time , while the light red function has weights to produce an estimate at time .
Timestepping table from Shchepetkin and McWilliams (2008a):
| SCRUM 3.0 | Rutgers | AGRIF | UCLA | Non-hydrostatic | |
|---|---|---|---|---|---|
| barotropic
mode |
LF-TR | LF-AM3 with FB
feedback |
LF-AM3 with FB
feedback |
Gen. FB
(AB3-AM4) |
Gen. FB
(AB3-AM4) |
| 2-D , iter. | , (2) | 1.85, (2) | 1.85, (2) | 1.78, (1) | 1.78, (1) |
| 3-D momenta | AB3 | AB3 | LF-AM3 | LF-AM3 | AB3 (mod) |
| Tracers | AB3 | LF-TR | LF-AM3 | LF-AM3 | AB3 (mod) |
| internal
waves |
AB3 | Gen. FB
(AB3-TR) |
LF-AM3,
FB feedback |
LF-AM3,
FB feedback |
Gen. FB
(AB3-AM4) |
| , advect. | 0.72 | 0.72 | 1.587 | 1.587 | 0.78 |
| , Cor. | 0.72 | 0.72 | 1.587 | 1.587 | 0.78 |
| , int. w. | 0.72, (1) | 1.14, (1,2) | 1.85, (2) | 1.85, (2) | 1.78, (1) |
![]() Note:
The generalized FB barotropic mode was ported into the newest AGRIF code at the end of 2007.
Note:
The generalized FB barotropic mode was ported into the newest AGRIF code at the end of 2007.
The number in parentheses (e.g., 2) indicates the number of r.h.s. computations per time step. If there are two parenthesized number, the first one is for momenta, the second for tracers.
Conservation Properties
From Shchepetkin and McWilliams (2005), we have a tracer concentration equation in advective form:
| (1) |
and also a tracer concentration equation in conservation form:
| (2) |
The continuity equation:
| (3) |
can be used to get from one tracer equation to the other. As a consequence of eq. (1), if the tracer is spatially uniform, it will remain so regardless of the velocity field (constancy preservation). On the other hand, as a consequence of (2), the volume integral of the tracer concentration is conserved in the absence of internal sources and fluxes through the boundary. Both properties are valuable and should be retained when constructing numerical ocean models.
The semi-discrete form of the tracer equation is:
| (4) |
Here , and denote simple centered finite-difference approximations to , and with the differences taken over the distances , and , respectively. is the vertical distance from one point to another. , and represent averages taken over the distances , and .
The finite volume version of the same equation is no different, except that a quantity is defined as the volume-averaged concentration over the grid box :
The quantity is the flux through an interface between adjacent grid boxes.
This method of averaging was chosen because it internally conserves first moments in the model domain, although it is still possible to exchange mass and energy through the open boundaries. The method is similar to that used in Arakawa and Lamb; though their scheme also conserves enstrophy. Instead, we will focus on (nearly) retaining constancy preservation while coupling the barotropic (depth-integrated) equations and the baroclinic equations.
The timestep in eq. (4) is assumed to be from time to time , with the other terms being evaluated at time for second-order accuracy. Setting to 1 everywhere reduces eq. (4) to:
| (5) |
If this equation holds true for the step from time to time , then constancy preservation will hold.
In a hydrostatic model such as ROMS, the discrete continuity equation is needed to compute vertical velocity rather than grid-box volume (the latter is controlled by changes in in the barotropic mode computations). Here, is the finite-volume flux across the moving grid-box interface, vertically on the grid.
The vertical integral of the continuity equation (5), using the vertical boundary conditions on , is:
| (6) |
where is the surface elevation, is the total depth, and are the depth-integrated horizontal velocities. This equation and the corresponding 2-D momentum equations are timestepped on a shorter timestep than eq. (4) and the other 3-D equations. Due to the details in the mode coupling, it is only possible to maintain constancy preservation to the accuracy of the barotropic timesteps.
Depth-Integrated Equations
The depth average of a quantity is given by:
| (7) |
where the overbar indicates a vertically averaged quantity and
| (8) |
is the total depth of the water column. The vertical integral of the momentum equations are:
| (9) |
and
| (10) |
where includes the term, is the horizontal viscosity, and the vertical viscosity only contributes through the upper and lower boundary conditions. We also need the vertical integral of the continuity equation, shown above as eq. (6).
The presence of a free surface introduces waves which propagate at a speed of . These waves usually impose a more severe time-step limit than any of the internal processes. We have therefore chosen to solve the full equations by means of a split time step. In other words, the depth integrated equations (9), (10), and (6) are integrated using a short time step and the values of and are used to replace those found by integrating the full equations on a longer time step. A diagram of the barotropic time stepping is shown here:
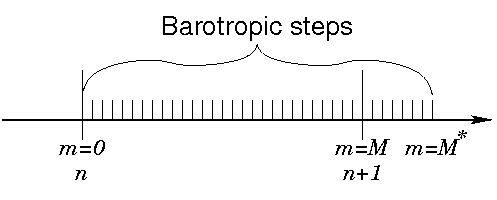
Some of the terms in equations (9) and (10) are updated on the short time step while others are not. The contributions from the slow terms are computed once per long time step and stored. If we call these terms and , equations (9) and (10) become:
| (11) |
and
| (12) |
When time stepping the model, we compute the right-hand-sides for the full 3-D momentum equations as well as the right-hand-sides for equations (11) and (12). The vertical integral of the 3-D right-hand-sides are obtained and then the 2-D right-hand-sides are subtracted. The resulting fields are the slow forcings and . This was found to be the easiest way to retain the baroclinic contributions of the non-linear terms such as .
The model is time stepped from time to time by using short time steps on equations (11), (12) and (6). Equation (6) is time stepped first, so that an estimate of the new is available for the time rate of change terms in equations (11) and (12). A third-order predictor-corrector time stepping is used. In practice, we actually time step all the way to time dtfast and while maintaining weighted averages of the values of , and . The averages are used to replace the values at time in both the baroclinic and barotropic modes, and for recomputing the vertical grid spacing . The following figure shows one option for how these weights might look:
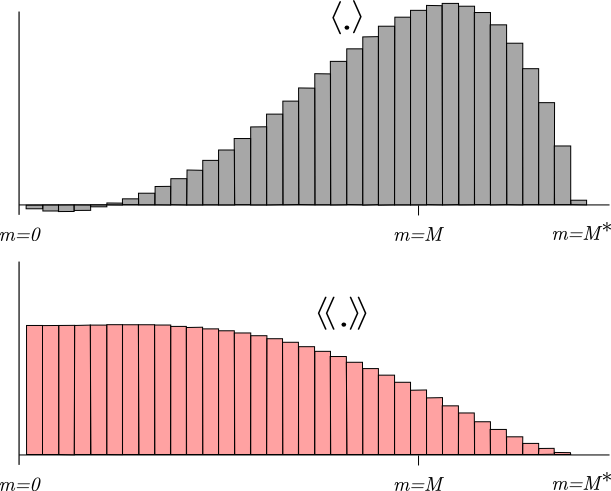
The primary weights, , are used to compute . There is a related set of secondary weights , used as . In order to maintain constancy preservation, this relation must hold:
| (13) |
Shchepetkin and McWilliams (2005) introduce a range of possible weights, but the ones used here have a shape function:
| (14) |
where are parameters and , and are chosen to satisfy normalization, consistency, and second-order accuracy conditions,
| (15) |
using Newton iterations. is the upper limit of with . In practice we initially set
compute using eq.~(14), normalize using:
| (16) |
and adjust iteratively to satisfy the condition of (15). We are using values of , , and . This form allows some negative weights for small , allowing to be less than .
ROMS also supports an older cosine weighting option, which isn't recommended since it is only first-order accurate.
Pressure Gradient Terms in Mode Coupling
Equation (11) contains the term , computed as the difference between the 3-D right-hand-side and the 2-D right-hand-side. The pressure gradient therefore has the form:
| (17) |
where the term in square brackets is the mode coupling term and is held fixed over all the barotropic steps and
| (18) |
is the vertically integrated pressure gradient. The latter is a function of the bathymetry, free surface gradient, and the free surface itself, as well as the vertical distribution of density.
The disadvantage of this approach is that after the barotropic time stepping is complete and the new free surface is substituted into the full baroclinic pressure gradient, its vertical integral will no longer be equal to the sum of the new surface slope term and the original coupling term based on the old free surface. This is one form of mode-splitting error which can lead to trouble because the vertically integrated pressure gradient is not in balance with the barotropic mass flux.
Instead, let us define the following:
| (19) |
Changing the vertical coordinate to yields:
| (20) |
which implies that and are actually independent of as long as the density profile does not change. The vertically integrated pressure gradient becomes:
| (21) |
In the case of uniform density , we obtain , but we otherwise have two new terms. The accuracy of these terms depends on an accurate vertical integration of the density, as described in Shchepetkin and McWilliams (2005).
Time Stepping: Internal Velocity Modes and Tracers
The momentum equations are advanced before the tracer equation, by computing all the terms except the vertical viscosity and then using the implicit scheme described in #Vertical Friction and Diffusion to find the new values for and . The depth-averaged component is then removed and replaced by the and computed as in #Depth-Integrated Equations. A third-order Adams-Bashforth (AB3) time step is used, requiring multiple right-hand-side time levels (see Time-stepping Schemes Review). These stored up r.h.s. values can be used to extrapolate to a value at time for use in the barotropic steps as shown in #Time-Stepping Overview.
The tracer concentration equation is advanced in a predictor-corrector leapfrog-trapezoidal step, with great care taken to optimize both the conservation and constancy-preserving properties of the continuous equations. The corrector step can maintain both, as long as it uses velocities and column depths which satisfy eq. (13). This also requires tracer values centered at time , obtained from the predictor step. The vertical diffusion is computed as in #Vertical Friction and Diffusion.
The predictor step cannot be both constancy-preserving and conservative; it was therefore decided to make it constancy-preserving. Also, since it is only being used to compute the advection for the corrector step, the expensive diffusion operations are not carried out on the predictor step.
![]() The preceeding notes on tracer advection refer to all but the MPDATA option. The MPDATA algorithm has its own predictor-corrector with emphasis on not allowing values to exceed their original range, and therefore gives up the constancy-preservation. This will be most noticeable in shallow areas with large tides.
The preceeding notes on tracer advection refer to all but the MPDATA option. The MPDATA algorithm has its own predictor-corrector with emphasis on not allowing values to exceed their original range, and therefore gives up the constancy-preservation. This will be most noticeable in shallow areas with large tides.
Horizontal and Vertical Advection
The advection of a tracer has an equation of the form
where we have introduced the advective fluxes:
Second-order Centered
The simplest form of the advective fluxes is the centered second-order:
This scheme is known to have some unfortunate properties in the presence of strong gradients, such as large over- and under-shoots of tracers, leading to the need for large amounts of horizontal smoothing. ROMS provides alternative advection schemes with better behavior in many situations, but retains this one for comparison purposes.
Fourth-order Centered
The barotropic advection is centered fourth-order unless you specifically pick centered second-order as your horizontal advection scheme. To get fourth-order, create gradient terms:
The fluxes now become:
| (22) |
Fourth-order Akima
An alternate fourth-order algorithm is that by Akima:
With the fluxes as in eq. (22).
Third-order Upwind
There is a class of third-order upwind advection schemes, both one-dimensional (Leonard, 1979) and two-dimensional (Rasch, 1994 and Shchepetkin and McWilliams, 1998). This scheme is known as UTOPIA (Uniformly Third-Order Polynomial Interpolation Algorithm). Applying flux limiters to UTOPIA is explored in Thuburn (1995), although it is not implemented in ROMS. The two-dimensional formulation in Rasch contains terms of order and , including cross terms (). The terms which are nonlinear in velocity have been dropped in ROMS, leaving one extra upwind term in the computation of the advective fluxes:
The second derivative terms are centered on a point in the grid, but are needed at a or point in the flux. The upstream value is used:
| (23) |
The value of in the model is while that in Rasch (1994) is .
Because the third-order upwind scheme is designed to be two-dimensional, it is not used in the vertical (though one might argue that we are simply performing one-dimensional operations here). Instead, we use a centered fourth-order scheme in the vertical when the third-order upwind option is turned on:
One advantage of UTOPIA over MPDATA is that it can be used on variables having both negative and positive values. Therefore, it can be used on velocity as well as scalars (is there a reference for this?). For the -velocity, we have:
while for the -velocity we have:
In all these terms, the second derivatives are evaluated at an upstream location.
MPDATA
Vertical Velocity
Having obtained a complete specification of the and fields at the next time level by the methods outlined above, the vertical velocity and density fields can be calculated. The vertical velocity is obtained by rewriting equation (5) as:
and combining it with equation (6) to obtain:
Solving for and using the semi-discrete notation we obtain:
The integral is actually computed as a sum from the bottom upwards and also as a sum from the top downwards. The value used is a linear combination of the two, weighted so that the surface down value is used near the surface while the other is used near the bottom. [Is this still done?]
Equation of State
The density is obtained from temperature and salinity via an equation of state. ROMS provides a choice of a nonlinear equation of state or a linear equation of state . The nonlinear equation of state has been modified and now corresponds to the UNESCO equation of state as derived by Jackett and McDougall (1995). It computes in situ density as a function of potential temperature, salinity and pressure.
Warning: although we have used it quite extensively in the past, McDougall (personal communication) claims that the single-variable () equation of state is not dynamically appropriate as is. He has worked out the extra source and sink terms required, arising from vertical motions and the compressibility of water. They are quite complicated and we have not implemented them to see if they alter the flow.
































































![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial t}}\left({\frac {D{\overline {u}}}{mn}}\right)+{\frac {\partial }{\partial \xi }}\left({\frac {D{\overline {uu}}}{n}}\right)+{\frac {\partial }{\partial \eta }}\left({\frac {D{\overline {uv}}}{m}}\right)-&{\frac {Df{\overline {v}}}{mn}}\\-\left[{\overline {vv}}{\frac {\partial }{\partial \xi }}\left({\frac {1}{n}}\right)-{\overline {uv}}{\frac {\partial }{\partial \eta }}\left({\frac {1}{m}}\right)\right]D=-{\frac {D}{n}}&\left({\frac {\partial {\overline {\phi _{2}}}}{\partial \xi }}+g{\frac {\partial \zeta }{\partial \xi }}\right)\\+{\frac {D}{mn}}\left({\overline {\cal {F}}}_{u}+{\overline {\cal {D}}}_{h_{u}}\right)&+{\frac {1}{mn}}\left(\tau _{s}^{\xi }-\tau _{b}^{\xi }\right)\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/ab720f2c158b841ade189c3a15fa813471c291cb)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial t}}\left({\frac {D{\overline {v}}}{mn}}\right)+{\frac {\partial }{\partial \xi }}\left({\frac {D{\overline {uv}}}{n}}\right)+{\frac {\partial }{\partial \eta }}\left({\frac {D{\overline {vv}}}{m}}\right)+&{\frac {Df{\overline {u}}}{mn}}\\+\left[{\overline {uv}}{\frac {\partial }{\partial \xi }}\left({\frac {1}{n}}\right)-{\overline {uu}}{\frac {\partial }{\partial \eta }}\left({\frac {1}{m}}\right)\right]D=-{\frac {D}{m}}&\left({\frac {\partial {\overline {\phi _{2}}}}{\partial \eta }}+g{\frac {\partial \zeta }{\partial \eta }}\right)\\+{\frac {D}{mn}}\left({\overline {\cal {F}}}_{v}+{\overline {\cal {D}}}_{h_{v}}\right)&+{\frac {1}{mn}}\left(\tau _{s}^{\eta }-\tau _{b}^{\eta }\right)\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/0d46d823c5dded802865e751a2f970f6fe4ef5fd)






![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial t}}\left({\frac {D{\overline {u}}}{mn}}\right)+{\frac {\partial }{\partial \xi }}\left({\frac {D{\overline {u}}\,{\overline {u}}}{n}}\right)+{\frac {\partial }{\partial \eta }}\left({\frac {D{\overline {u}}\,{\overline {v}}}{m}}\right)&-{\frac {Df{\overline {v}}}{mn}}\\-\left[{\overline {v}}\,{\overline {v}}{\frac {\partial }{\partial \xi }}\left({\frac {1}{n}}\right)-{\overline {u}}\,{\overline {v}}{\frac {\partial }{\partial \eta }}\left({\frac {1}{m}}\right)\right]D&=R_{u_{\rm {slow}}}-{\frac {gD}{n}}{\frac {\partial \zeta }{\partial \xi }}+{\frac {D}{mn}}{\cal {D}}_{\overline {u}}-{\frac {1}{mn}}\tau _{b}^{\xi }\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/ed7b350533209b58ef900c7a9ee72d26b20416e0)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial t}}\left({\frac {D{\overline {v}}}{mn}}\right)+{\frac {\partial }{\partial \xi }}\left({\frac {D{\overline {u}}\,{\overline {v}}}{n}}\right)+{\frac {\partial }{\partial \eta }}\left({\frac {D{\overline {v}}\,{\overline {v}}}{m}}\right)&+{\frac {Df{\overline {u}}}{mn}}\\+\left[{\overline {u}}\,{\overline {v}}{\frac {\partial }{\partial \xi }}\left({\frac {1}{n}}\right)-{\overline {u}}\,{\overline {u}}{\frac {\partial }{\partial \eta }}\left({\frac {1}{m}}\right)\right]D&=R_{v_{\rm {slow}}}-{\frac {gD}{m}}{\frac {\partial \zeta }{\partial \eta }}+{\frac {D}{mn}}{\cal {D}}_{\overline {v}}-{\frac {1}{mn}}\tau _{b}^{\eta }.\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/5f6b6b3f49d6a98b5fb942ba5b5fbf95dad45aae)









![{\displaystyle {\begin{aligned}\langle \zeta \rangle _{i,j}^{n+1}=\langle \zeta \rangle _{i,j}^{n}&-\\(mn)_{i,j}\Delta t&\left[\left\langle \!\!\left\langle {\frac {D{\overline {u}}}{n}}\right\rangle \!\!\right\rangle _{i+{\frac {1}{2}},j}^{n+{\frac {1}{2}}}-\left\langle \!\!\left\langle {\frac {D{\overline {u}}}{n}}\right\rangle \!\!\right\rangle _{i-{\frac {1}{2}},j}^{n+{\frac {1}{2}}}+\left\langle \!\!\left\langle {\frac {D{\overline {v}}}{m}}\right\rangle \!\!\right\rangle _{i,j+{\frac {1}{2}}}^{n+{\frac {1}{2}}}-\left\langle \!\!\left\langle {\frac {D{\overline {v}}}{m}}\right\rangle \!\!\right\rangle _{i,j-{\frac {1}{2}}}^{n+{\frac {1}{2}}}\right]\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/8e7e2e9a6d4511a448bb1f166f62a5a418ba2307)
![{\displaystyle A(\tau )=A_{0}\left\{\left({\frac {\tau }{\tau _{0}}}\right)^{p}\left[1-\left({\frac {\tau }{\tau _{0}}}\right)^{q}\right]-r{\frac {\tau }{\tau _{0}}}\right\}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/cf3d35e9d22b47b0b59fa638147dcef4f948a372)

















![{\displaystyle -{\frac {gD}{n}}{\frac {\partial \zeta }{\partial \xi }}+\left[{\frac {gD}{n}}{\frac {\partial \zeta }{\partial \xi }}+{\cal {F}}\right]}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/f8bf2483e4b5c737bdc706c6cb5fae2248cc261b)






















![{\displaystyle F_{i,j,k}^{\xi }={\frac {{\overline {H_{z}}}^{\xi }}{{\overline {n}}^{\xi }}}\left[\max(0,u_{i,j,k})C_{i-1,j,k}+\min(0,u_{i,j,k})C_{i,j,k}\right].}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/361ae425f8108e971599eacd6a71f2e5c32200b4)



![{\displaystyle F^{s}={\frac {H_{z}w}{mn}}\left[-{\frac {1}{16}}C_{i,j,k-1}+{\frac {9}{16}}C_{i,j,k}+{\frac {9}{16}}C_{i,j,k+1}-{\frac {1}{16}}C_{i,j,k+2}\right]}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/e868f0035b171eda0a173b61c2487934bad06f8b)
![{\displaystyle {\begin{aligned}F^{\xi }&=\left(u-\gamma {\frac {\partial ^{2}u}{\partial \xi ^{2}}}\right)\left[{\frac {H_{z}u}{n}}-\gamma {\frac {\partial ^{2}}{\partial \xi ^{2}}}\left({\frac {H_{z}u}{n}}\right)\right]\\F^{\eta }&=\left(u-\gamma {\frac {\partial ^{2}u}{\partial \eta ^{2}}}\right)\left[{\frac {H_{z}v}{m}}-\gamma {\frac {\partial ^{2}}{\partial \xi ^{2}}}\left({\frac {H_{z}v}{m}}\right)\right]\\F^{\sigma }&={\frac {H_{z}w}{mn}}\left[-{\frac {1}{16}}u_{i,j,k-1}+{\frac {9}{16}}u_{i,j,k}+{\frac {9}{16}}u_{i,j,k+1}-{\frac {1}{16}}u_{i,j,k+2}\right]\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/796cb7d7e40de603d899dad15b5655ca289714e7)
![{\displaystyle {\begin{aligned}F^{\xi }&=\left(v-\gamma {\frac {\partial ^{2}v}{\partial \xi ^{2}}}\right)\left[{\frac {H_{z}u}{n}}-\gamma {\frac {\partial ^{2}}{\partial \eta ^{2}}}\left({\frac {H_{z}u}{n}}\right)\right]\\F^{\eta }&=\left(v-\gamma {\frac {\partial ^{2}v}{\partial \eta ^{2}}}\right)\left[{\frac {H_{z}v}{m}}-\gamma {\frac {\partial ^{2}}{\partial \eta ^{2}}}\left({\frac {H_{z}v}{m}}\right)\right]\\F^{\sigma }&={\frac {H_{z}w}{mn}}\left[-{\frac {1}{16}}v_{i,j,k-1}+{\frac {9}{16}}v_{i,j,k}+{\frac {9}{16}}v_{i,j,k+1}-{\frac {1}{16}}v_{i,j,k+2}\right]\end{aligned}}}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/f64311e7a56cc27088910b710c544a67efbd60a4)




![{\displaystyle {\frac {H_{z}\Omega }{mn}}=\int \left[\delta _{\xi }\left({\frac {{\overline {u}}{\overline {D}}^{\xi }}{{\overline {n}}^{\xi }}}\right)+\delta _{\eta }\left({\frac {{\overline {v}}{\overline {D}}^{\eta }}{{\overline {m}}^{\eta }}}\right)-\delta _{\xi }\left({\frac {u{\overline {H_{z}}}^{\xi }}{{\overline {n}}^{\xi }}}\right)-\delta _{\eta }\left({\frac {v{\overline {H_{z}}}^{\eta }}{{\overline {m}}^{\eta }}}\right)\right]d\sigma .}](https://www.myroms.org/www.myroms.org/v1/media/math/render/svg/6694c4b4a430c33c4569078ba93d7a4faaedce9a)

