LAKE SIGNELL CASE
This case provides a fundamental check of the ability of a model to represent 1) wind driven transport in a closed basin, 2) wave-current influences on bottom friction and sediment resuspension, 3) flux of two grain sizes from the bed, and 4) resuspension, transport, and deposition of suspended-sediment. Lake Signell derives its name from the paper by Signell et al. (1990).
Domain
The domain is an enclosed basin, rectangular in plan view, with a sloping bottom.
Model Parameter Variable Value Length (east-west) l 50000 m Width (north-south) w 10000 m Depth h 18 m at the northern end, decreasing linearly to 2 m at the southern end
Bottom Sediment
Size D50 0.1 mm Density ρs 2650 kg/m3 Settling Velocity ws 0.1 mm/s Critical Shear Stress τc 0.05 N/m2 Bed Thickness bed_thick 0.005 mm Erosion Rate E0 5e-5 kg/m2/s
Forcing
No Coriolis
No heating/cooling
Wind:
- Wind speed = , blowing along the lake to the east
Waves:
- RMS wave height =
- Period =
- Direction: propagating in wind direction
Initial Conditions
Salinity =
Boundary Conditions
North, south, east, and west sides = walls with no fluxes, no friction
Bottom roughness in absence of waves
Surface roughness
Sediment flux calculated by model
Surface = free surface, no fluxes of heat or salt (momentum fluxes associated with wind)
Physical Constants
Gravitational acceleration
Von Karman's constant
Dynamic viscosity (and minimum diffusivity)
![]() Note:
If a model incorporates physical constants that differ from these, and/or automatically calculates some values specified here, please specify the values used.
Note:
If a model incorporates physical constants that differ from these, and/or automatically calculates some values specified here, please specify the values used.
Results
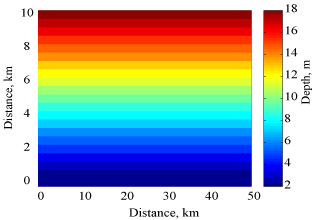
Model bathymetry has a sloping bottom as shown in figure 1. Simulations were conducted for 3.0 days. For this simulation, the bottom orbital velocities, wave period, and direction were obtained from a steady-state solution of the model SWAN. For the hydrodynamic simulation, the wave field results from SWAN were increased from 0 to their maximum values with a hyperbolic tangent function that reached maximum value at 10 hours. The surface stress was held constant until a total of 40 hours have elapsed, when the stress was decreased hyperbolically for 10 hours. The simulation continued until all sediment had settled from the water column.
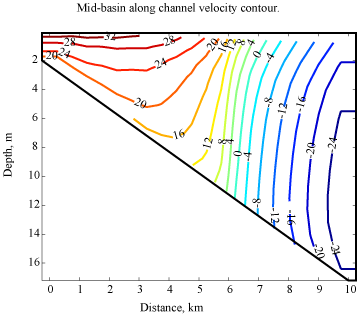
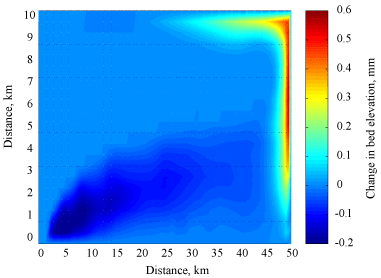
Cross sectional plot of velocity contours at x = 25 km is shown in figure 2, at maximum wind stress. A downwind surface flow of near 32 cm/s is observed in the shallow region, with a compensating upwind flow at depth of 24 cm/s. Figure 3 shows the final bathymetric change. The majority of the sediment was transport from the southwest corner towards the northeast corner, due to the counter clockwise circulation from the westerly wind stress.