Vertical S-coordinate
<wikitex> Following Song and Haidvogel (1994) but modified by Shchepetkin and McWilliams (2005), the vertical coordinate has been chosen to be:
$$z = \zeta + \left(1 + {\zeta \over h} \right) \left[h_c \sigma + (h - h_c) C(\sigma)\right],
\qquad \qquad -1 \leq \sigma \leq 0$$
where $h_c$ is either the minimum depth or a shallower depth above which we wish to have more resolution. $C(\sigma)$ is defined as:
$$C(\sigma) = (1 - b) {\sinh (\theta \sigma) \over \sinh \theta } +
b { \tanh [\theta ( \sigma + {1\over 2})] -
\tanh ( {1\over 2} \theta) \over
2 \tanh ( {1\over 2} \theta) }$$
where $\theta$ and $b$ are surface and bottom control parameters. Their ranges are $0 < \theta \leq 20$ and $0 \leq b \leq 1$, respectively. The first equation leads to $z = \zeta$ for $\sigma = 0$ and $z = h$ for $\sigma = -1$.
Some features of this coordinate system:
- It is a generalization of the traditional $\sigma$-coordinate system. Letting $\theta$ go to zero and using L'Hopital's rule, we get:
$$z = (\zeta + h)(1 + \sigma) - h$$
which is the traditional $\sigma$-coordinate.
- It is infinitely differentiable in $\sigma$.
- The larger the value of $\theta$, the more resolution is kept above $h_c$.
- For $b = 0$, the resolution all goes to the surface as $\theta$ is increased.
- For $b = 1$, the resolution goes to both the surface and the bottom equally as $\theta$ is increased.
- For $\theta \neq 0$ there is a subtle mismatch in the discretization of the model equations, for instance in the horizontal viscosity term. We recommend that you stick with "reasonable" values of $\theta$, say $\theta \leq 8$.
- Some problems turn out to be sensitive to the value of $\theta$ used.
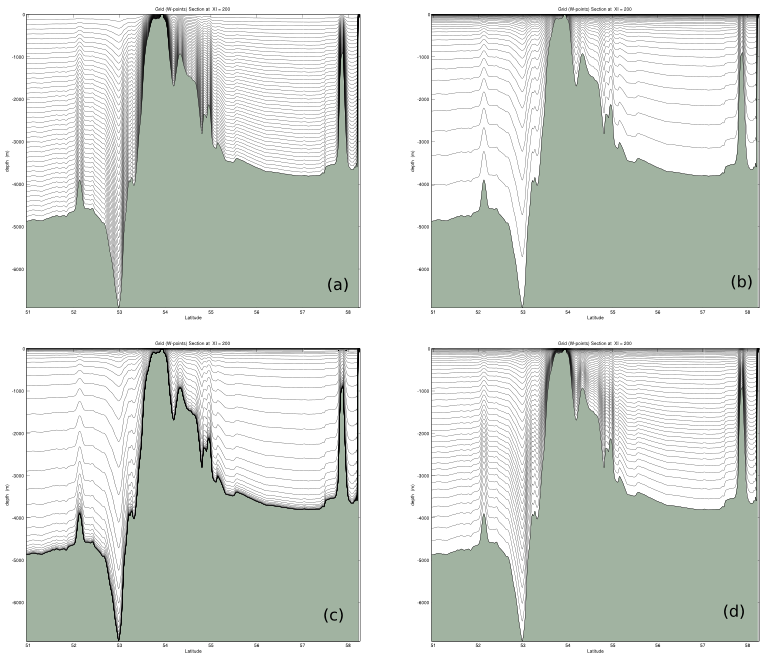
The following figure shows the $\sigma$-surfaces for several values of $\theta$ and $b$ for one of our domains. It was produced by a Matlab tool written by Hernan Arango which is available from our web site.
Figure: The $\sigma$-surfaces for the North Atlantic with (a) $\theta = 0.0001$ and $b = 0$, (b) $\theta = 8$ and $b = 0$, (c) $\theta = 8$ and $b = 1$. (d) The actual values used in this domain were $\theta = 5$ and $b = 0.4$.
We find it convenient to define: $$H_z \equiv {\partial z \over \partial \sigma}$$
The derivative of $C(\sigma)$ can be computed analytically:
$${\partial C(\sigma) \over \partial \sigma} = (1-b) {\cosh (\theta \sigma) \over
\sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over
2 \cosh^2 [ \theta (\sigma + {1\over 2})] } \theta$$
However, we choose to compute $H_z$ discretely as $\Delta z/ \Delta \sigma$ since this leads to the vertical sum of $H_z$ being exactly the total water depth $D$.
Note that though we have used this form of $\sigma$-coordinate, ROMS is written in such a way as to work with a variety of vertical mappings. There is one feature which is critical however. If free surface is at rest, $\zeta = 0$, you get one solution for the level depths $z^{(0)}(k)$. In the case of nonzero $\zeta$, the displacements must be proportional to $\zeta$ and to the original distance from the bottom:
$$ z(k) = z^{(0)} (k) + \zeta \left( 1 + {z^{(0)} (k) \over h} \right) $$
or
$$ \Delta z(k) = \Delta z^{(0)} (k) \left( 1 + {\zeta \over h} \right) $$
This ensures that the vertical mass fluxes generated by a purely barotropic motion will vanish at every interface. </wikitex>