TEST HEAD CASE
This test case checks the ability of a model to represent 1) simplified alongshore transport, 2) implementation of open boundary conditions, and 3) resuspension, transport, and deposition of suspended-sediment. This case is based on Signell and Geyer (1991).
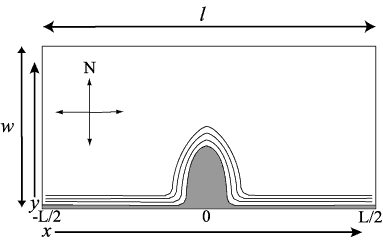
Domain
The model domain is open at the east and west ends, has a straight wall at the north end, and a parabolic headland along the south wall.
Model Parameter Variable Value Length (east-west) l 100000 m Width (north-south) w 50000 m Depth h 20 m
Bottom Sediment
Single grain size on bottom:
Model Parameter Variable Value Size D50 0.1 mm Density ρs 2650 kg/m3 Settling Velocity ws 0.50 mm/s Critical shear stress τc 0.05 N/m2 Bed thickness bed_thick 0.005 m Erosion Rate E0 5e-5 kg/m2/s
Forcing
<wikitex>Coriolis $\textcolor{blue}{f}~ =~ 1.0~ e^{-4}$</wikitex>
No heating/cooling
No wind
Initial Conditions
<wikitex>$\textcolor{blue}{u}~ =~ 0~ m^{3}$
$Salinity~ =~ 0$
$\textcolor{blue}{Temperature}~ =~ 20^{\circ}C$</wikitex>
Bathymetry:
Depths increase linearly (slope = 0.0067) from a minimum depth of 2 m at all alongshore points from the southern land boundary offshore to a maximum depth of 20 m at a point 3 km offshore. Offshore of 3 km there is a constant depth of 20 m.
Boundary Conditions
North, south = walls with no fluxes, no friction
South wall = parabolic headland shape
<wikitex>Bottom roughness $\textcolor{blue}{Z_{\circ}}~ =~ 0.015~ m$
Flow and elevation at western boundary is imposed.
Flow on eastern boundary is open radiation condition, or water level based, or Kelvin wave solution.
Flow and elevation, eastern/western boundaries:
Reference velocity $\textcolor{blue}{u_{\circ}}~ =~ 0.5~ m/s$
Celerity $\textcolor{blue}{C}~=~ \sqrt{(\textcolor{blue}{g}\times 20.0)}$
Reference water level $\textcolor{blue}{\xi_{\circ}}~ =~\textcolor{blue}{u_{\circ}}/\sqrt{(\textcolor{blue}{g}/20)}$
Wave period $\textcolor{blue}{T}~ =~ 12$ hours (43200 seconds)
Wave length $\textcolor{blue}{L}~ = \textcolor{blue}{C}\times \textcolor{blue}{T}$
Wave number $\textcolor{blue}{k}~ =~ (2\times\pi)/\textcolor{blue}{L}$</wikitex>
<wikitex>For each point $y$ along the boundary at time $\textcolor{blue}{t}$:
Water level $\textcolor{blue}{\xi}~ =~\textcolor{blue}{\xi_{\circ}}\times exp(\textcolor{blue}{-f}\times y/\textcolor{blue}{C}) \times cos(\textcolor{blue}{k} \times (x - \textcolor{blue}{C} \times \textcolor{blue}{t}))$</wikitex>
![]() Note: <wikitex>$x$ at western boundary is $\textcolor{blue}{-L}/2$
Note: <wikitex>$x$ at western boundary is $\textcolor{blue}{-L}/2$
Depth-mean flow $\textcolor{blue}{}~ =~ \sqrt{(\textcolor{blue}{g}/20)} \times \textcolor{blue}{\xi}(y)$</wikitex>
Sediment flux calculated by model
Surface = free surface, no fluxes
Output (ASCII files suitable for plotting)
After 10 days :
Bed thickness
Physical Constants
<wikitex>Gravitational acceleration $\textcolor{blue}{g}~ =~ 9.81~ m/s^{2}$
Von Karman's constant $\textcolor{blue}{\kappa}~=~ 0.41$
Dynamic viscosity (and minimum diffusivity) $\textcolor{blue}{\nu}~ =~ 1e^{-6}~ m^{2}/s$</wikitex>
If a model incorporates physical constants that differ from these, and/or automatically calculates some values specified here, please specify the values used.
Results
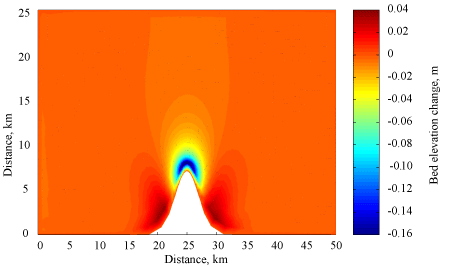
Simulations were conducted for 3.0 days. Final bed thickness is shown in Figure 1.