Vertical S-coordinate: Difference between revisions
No edit summary (change visibility) |
|||
| Line 10: | Line 10: | ||
<wikitex> | <wikitex> | ||
The following vertical coordinate transformations are available: | The following vertical coordinate transformations are available: | ||
<span id="transform1"></span> | |||
$$ \eqalign { | $$ \eqalign { | ||
z(x,y,\sigma,t) &= S(x,y,\sigma) + \zeta(x,y,t) \left[1 + \frac{S(x,y,\sigma)}{h(x,y)}\right], \cr | z(x,y,\sigma,t) &= S(x,y,\sigma) + \zeta(x,y,t) \left[1 + \frac{S(x,y,\sigma)}{h(x,y)}\right], \cr | ||
| Line 17: | Line 17: | ||
or | or | ||
<span id="transform2"></span> | |||
$$ \eqalign { | $$ \eqalign { | ||
z(x,y,\sigma,t) &= \zeta(x,y,t) + \left[\zeta(x,y,t) + h(x,y)\right] \, S(x,y,\sigma), \cr | z(x,y,\sigma,t) &= \zeta(x,y,t) + \left[\zeta(x,y,t) + h(x,y)\right] \, S(x,y,\sigma), \cr | ||
| Line 30: | Line 30: | ||
affected by erosion and deposition processes. | affected by erosion and deposition processes. | ||
{{note}} Transformation (1) has been available in ROMS since 1999. It is activated by setting [[Variables#Vtransform|Vtransform = 1]] in [[ocean.in]]. | {{note}} Transformation [[#transform1|(1)]] has been available in ROMS since 1999. It is activated by setting [[Variables#Vtransform|Vtransform = 1]] in [[ocean.in]]. Notice that, | ||
$$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | $$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | ||
| Line 39: | Line 39: | ||
displacements of the free-surface. | displacements of the free-surface. | ||
{{note}} Transformation (2) has been available in UCLA-ROMS for awhile. It is activated by setting [[Variables#Vtransform|Vtransform = 2]] in [[ocean.in]]. | {{note}} Transformation [[#transform2|(2)]] has been available in UCLA-ROMS for awhile. It is activated by setting [[Variables#Vtransform|Vtransform = 2]] in [[ocean.in]]. Notice that, | ||
$$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | $$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | ||
-1, &if $\;\;\sigma = -1, \;\; C(\sigma) = -1$, \qquad\hbox{at the ocean bottom;}\cr}$$ | -1, &if $\;\;\sigma = -1, \;\; C(\sigma) = -1$, \qquad\hbox{at the ocean bottom;}\cr}$$ | ||
which is different to the behavior of the original functional in (1). Shchepetkin (personal communication) points out that (2) offers | which is different to the behavior of the original functional in (1). Shchepetkin (personal communication) points out that (2) offers couple of advantages: | ||
couple of advantages: | |||
* Regardless of the design of $C(\sigma)$, transformation (2) behaves like equally-spaced sigma-coordinates in shallow regions, where $h(x,y) \ll h_c$. This is advantageous because it avoids excessive resolution and associated CFL limitation is such areas. | * Regardless of the design of $C(\sigma)$, transformation (2) behaves like equally-spaced sigma-coordinates in shallow regions, where $h(x,y) \ll h_c$. This is advantageous because it avoids excessive resolution and associated CFL limitation is such areas. | ||
| Line 69: | Line 68: | ||
is defined in terms of several parameters which are specified in standard input file [[ocean.in]]. | is defined in terms of several parameters which are specified in standard input file [[ocean.in]]. | ||
'''Stretching Function Properties:''' | |||
* a dimensionless, nonlinear, monotonic function; | * $C(\sigma)$ is a dimensionless, nonlinear, monotonic function; | ||
* a continuous differentiable function, or a piecewise function with smooth transition and differentiable; | * $C(\sigma)$ is a continuous differentiable function, or a piecewise function with smooth transition and differentiable; | ||
* must be discritized in terms of the fractional stretched vertical coordinate $\sigma$, | * $C(\sigma)$ must be discritized in terms of the fractional stretched vertical coordinate $\sigma$, | ||
$$ \sigma(k) = \cases{\frac{k-N}{N}, &at vertical $W\hbox{-points}, \;k=0,\dots,N$, \cr\cr | $$ \sigma(k) = \cases{\frac{k-N}{N}, &at vertical $W\hbox{-points}, \;k=0,\dots,N$, \cr\cr | ||
\frac{k-N-0.5}{N}, &at vertical $\rho\hbox{-points}, \;\;\;k=1,\dots,N$ \cr}$$ | \frac{k-N-0.5}{N}, &at vertical $\rho\hbox{-points}, \;\;\;k=1,\dots,N$ \cr}$$ | ||
* must be constrained by $-1 \le C(\sigma) \le 0$, that is, | * $C(\sigma)$ must be constrained by $-1 \le C(\sigma) \le 0$, that is, | ||
$$ C(\sigma) = \cases{0, &for $\;\;\sigma = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | $$ C(\sigma) = \cases{0, &for $\;\;\sigma = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr | ||
Revision as of 17:17, 4 March 2009
<wikitex> ROMS has a generalized vertical, terrain-following, coordinate system. Currently, two vertical transformation equations, $z=z(x,y,\sigma,t)$, are available which can support numerous vertical stretching 1D-functions when several constraints are satisfied. </wikitex>
Transformation Equations
<wikitex> The following vertical coordinate transformations are available: $$ \eqalign {
z(x,y,\sigma,t) &= S(x,y,\sigma) + \zeta(x,y,t) \left[1 + \frac{S(x,y,\sigma)}{h(x,y)}\right], \cr
\noalign{\medskip}
S(x,y,\sigma) &= h_c \, \sigma + \left[h(x,y) - h_c\right] \, C(\sigma) } \eqno{(1)} $$
or $$ \eqalign {
z(x,y,\sigma,t) &= \zeta(x,y,t) + \left[\zeta(x,y,t) + h(x,y)\right] \, S(x,y,\sigma), \cr
\noalign{\medskip}
S(x,y,\sigma) &= \frac{h_c \, \sigma + h(x,y)\, C(\sigma)}{h_c + h(x,y)} } \eqno{(2)} $$
where $S(x,y,\sigma)$ is a nonlinear vertical transformation functional, $\zeta(x,y,t)$ is the time-varying free-surface, $h(x,y)$ is the unperturbed water column thickness and $z=-h(x,y)$ corresponds to the ocean bottom, $\sigma$ is a fractional vertical stretching coordinate ranging from $-1 \le\sigma\le 0$, $C(\sigma)$ is a nondimensional, monotonic, vertical stretching function ranging from $-1 \le C(\sigma) \le 0$, and $h_c$ is a positive critical depth or thickness controlling the stretching. In sediment applications, $h=h(x,y,t)$ is changed at every time-step since it is affected by erosion and deposition processes.
![]() Transformation (1) has been available in ROMS since 1999. It is activated by setting Vtransform = 1 in ocean.in. Notice that,
Transformation (1) has been available in ROMS since 1999. It is activated by setting Vtransform = 1 in ocean.in. Notice that,
$$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr
-h(x,y), &if $\;\;\sigma = -1, \;\; C(\sigma) = -1$, \qquad\hbox{at the ocean bottom.}\cr}$$
In an undisturbed ocean state, corresponding to zero free-surface, $z=S(x,y,\sigma)$. Shchepetkin and McWilliams (2005) denotes this transformation as an unperturbed coordinate system since all the depths are not affected by the displacements of the free-surface.
![]() Transformation (2) has been available in UCLA-ROMS for awhile. It is activated by setting Vtransform = 2 in ocean.in. Notice that,
Transformation (2) has been available in UCLA-ROMS for awhile. It is activated by setting Vtransform = 2 in ocean.in. Notice that,
$$ S(x,y,\sigma) = \cases{0, &if $\;\;\sigma = \phantom{-}0, \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr
-1, &if $\;\;\sigma = -1, \;\; C(\sigma) = -1$, \qquad\hbox{at the ocean bottom;}\cr}$$
which is different to the behavior of the original functional in (1). Shchepetkin (personal communication) points out that (2) offers couple of advantages:
- Regardless of the design of $C(\sigma)$, transformation (2) behaves like equally-spaced sigma-coordinates in shallow regions, where $h(x,y) \ll h_c$. This is advantageous because it avoids excessive resolution and associated CFL limitation is such areas.
- Near-surface refinement behaves more or less like geopotential coordinates in deep regions (level thicknesses, $H_z$, do not depend or weakly depend on bathymetry), while near-bottom like sigma coordinates ($H_z$ is roughly proportional to depth). This reduces the extreme r-factors near the bottom and reduces pressure gradient errors.
In an undisturbed ocean state, $\zeta\equiv 0$, transformation (2) yields the following unperturbed depths, $\hat{z}$,
$$ \hat{z}(x,y,\sigma) \equiv h(x,y) \, S(x,y,\sigma) = h(x,y) \left[\frac{h_c \, \sigma + h(x,y)\, C(\sigma)}{h_c + h(x,y)}\right] \eqno{(3)} $$
and
$$ d\hat{z} = d\sigma \; h(x,y) \; \left[\frac{h_c}{h_c + h(x,y)}\right] \eqno{(4)} $$
As a consequence, the uppermost grid box retains very little dependency from bathymetry in deep areas, where $h_c \ll h(x,y)$. For example, if $h_c = 250\,m$ and $h(x,y)$ changes from $2000$ to $6000\,m$, the uppermost grid box changes only by a factor of 1.08 (less than $10\%$). </wikitex>
Vertical Stretching Functions
<wikitex> The above generic vertical transformation design facilitates numerous vertical stretching functions, $C(\sigma)$. This function is defined in terms of several parameters which are specified in standard input file ocean.in.
Stretching Function Properties:
- $C(\sigma)$ is a dimensionless, nonlinear, monotonic function;
- $C(\sigma)$ is a continuous differentiable function, or a piecewise function with smooth transition and differentiable;
- $C(\sigma)$ must be discritized in terms of the fractional stretched vertical coordinate $\sigma$,
$$ \sigma(k) = \cases{\frac{k-N}{N}, &at vertical $W\hbox{-points}, \;k=0,\dots,N$, \cr\cr
\frac{k-N-0.5}{N}, &at vertical $\rho\hbox{-points}, \;\;\;k=1,\dots,N$ \cr}$$
- $C(\sigma)$ must be constrained by $-1 \le C(\sigma) \le 0$, that is,
$$ C(\sigma) = \cases{0, &for $\;\;\sigma = \phantom{-}0, \qquad\hbox{at the free-surface;}$\cr
-1, &for $\;\;\sigma = -1, \qquad\hbox{at the ocean bottom.}$\cr}$$
Following Song and Haidvogel (1994) but modified by Shchepetkin and McWilliams (2005), the vertical coordinate has been chosen to be:
$$z = \zeta + \left(1 + {\zeta \over h} \right) \left[h_c \sigma + (h - h_c) C(\sigma)\right],
\qquad \qquad -1 \leq \sigma \leq 0$$
where $h_c$ is either the minimum depth or a shallower depth above which we wish to have more resolution. $C(\sigma)$ is defined as:
$$C(\sigma) = (1 - b) {\sinh (\theta \sigma) \over \sinh \theta } +
b { \tanh [\theta ( \sigma + {1\over 2})] -
\tanh ( {1\over 2} \theta) \over
2 \tanh ( {1\over 2} \theta) }$$
where $\theta$ and $b$ are surface and bottom control parameters. Their ranges are $0 < \theta \leq 20$ and $0 \leq b \leq 1$, respectively. The first equation leads to $z = \zeta$ for $\sigma = 0$ and $z = h$ for $\sigma = -1$.
Some features of this coordinate system:
- It is a generalization of the traditional $\sigma$-coordinate system. Letting $\theta$ go to zero and using L'Hopital's rule, we get:
$$z = (\zeta + h)(1 + \sigma) - h$$
which is the traditional $\sigma$-coordinate.
- It is infinitely differentiable in $\sigma$.
- The larger the value of $\theta$, the more resolution is kept above $h_c$.
- For $b = 0$, the resolution all goes to the surface as $\theta$ is increased.
- For $b = 1$, the resolution goes to both the surface and the bottom equally as $\theta$ is increased.
- For $\theta \neq 0$ there is a subtle mismatch in the discretization of the model equations, for instance in the horizontal viscosity term. We recommend that you stick with "reasonable" values of $\theta$, say $\theta \leq 8$.
- Some problems turn out to be sensitive to the value of $\theta$ used.
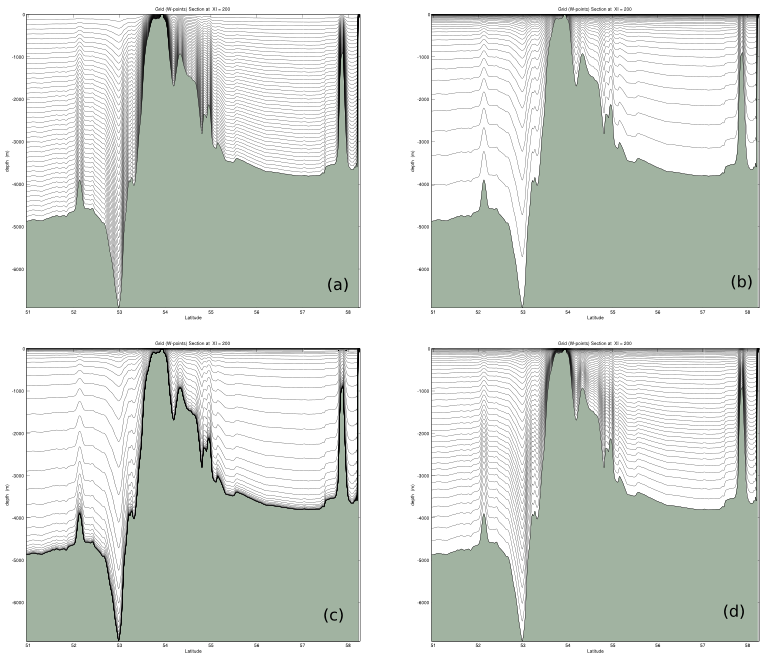
The following figure shows the $\sigma$-surfaces for several values of $\theta$ and $b$ for one of our domains. It was produced by a Matlab tool written by Hernan Arango which is available from our web site.
Figure: The $\sigma$-surfaces for the North Atlantic with (a) $\theta = 0.0001$ and $b = 0$, (b) $\theta = 8$ and $b = 0$, (c) $\theta = 8$ and $b = 1$. (d) The actual values used in this domain were $\theta = 5$ and $b = 0.4$.
We find it convenient to define: $$H_z \equiv {\partial z \over \partial \sigma}$$
The derivative of $C(\sigma)$ can be computed analytically:
$${\partial C(\sigma) \over \partial \sigma} = (1-b) {\cosh (\theta \sigma) \over
\sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over
2 \cosh^2 [ \theta (\sigma + {1\over 2})] } \theta$$
However, we choose to compute $H_z$ discretely as $\Delta z/ \Delta \sigma$ since this leads to the vertical sum of $H_z$ being exactly the total water depth $D$.
Note that though we have used this form of $\sigma$-coordinate, ROMS is written in such a way as to work with a variety of vertical mappings. There is one feature which is critical however. If the free surface is at rest, $\zeta = 0$, you get one solution for the level depths $z^{(0)}(k)$. In the case of nonzero $\zeta$, the displacements must be proportional to $\zeta$ and to the original distance from the bottom:
$$ z(k) = z^{(0)} (k) + \zeta \left( 1 + {z^{(0)} (k) \over h} \right) $$
or
$$ \Delta z(k) = \Delta z^{(0)} (k) \left( 1 + {\zeta \over h} \right) $$
This ensures that the vertical mass fluxes generated by a purely barotropic motion will vanish at every interface. </wikitex>