Vertical S-coordinate

Vertical S-coordinate

<wikitex> ROMS has a generalized vertical, terrain-following, coordinate system. Currently, two vertical transformation equations, $z=z(x,y,s,t)$, are available which may support numerous vertical stretching 1D-functions if several constraints are satisfied. </wikitex>

Transformation Equations

<wikitex> The following vertical coordinate transformations are available:

$$ \eqalign {

     z(x,y,\sigma,t) &= S(x,y,\sigma) + \zeta(x,y,t) \left[1 + \frac{S(x,y,\sigma)}{h(x,y)}\right], \cr
  \noalign{\medskip}
       S(x,y,\sigma) &= h_c \, \sigma + \left[h(x,y) - h_c\right] \, C(\sigma) } \eqno{(1)} $$

or

$$ \eqalign {

     z(x,y,\sigma,t) &= \zeta(x,y,t) + \left[\zeta(x,y,t) + h(x,y)\right] \, S(x,y,\sigma), \cr
  \noalign{\medskip}
       S(x,y,\sigma) &= \frac{h_c \, \sigma + h(x,y)\, C(\sigma)}{h_c + h(x,y)} } \eqno{(2)} $$

where $S(x,y,\sigma)$ is a nonlinear vertical transformation functional, $\zeta(x,y,t)$ is the time-varying free-surface, $h(x,y)$ is the unperturbed water column thickness and $z=-h(x,y)$ corresponds to the ocean bottom, $\sigma$ is a fractional vertical stretching coordinate ranging from $-1 \le\sigma\le 0$, $C(\sigma)$ is a nondimensional, monotonic, vertical stretching function ranging from $-1 \le C(\sigma) \le 0$, and $h_c$ is a positive critical depth or thickness controlling the stretching. In sediment applications, $h=h(x,y,t)$ is changed at every time-step since it is affected by erosion and deposition processes.

The transformation (1) has been available in ROMS since 1999. Notice that,

$$ S(x,y,\sigma) = \cases{0,        &if $\;\;\sigma = \phantom{-}0,  \;\; C(\sigma) = \phantom{-}0, \qquad\hbox{at the free-surface}$\cr
                          -h(x,y),  &if $\;\;\sigma = -1, \;\; C(\sigma) = -1$, \qquad\hbox{at the bottom}\cr}$$

</wikitex>

Vertical Stretching Functions

<wikitex> </wikitex>

Following Song and Haidvogel (1994) but modified by Shchepetkin and McWilliams (2005), the vertical coordinate has been chosen to be:

$$z = \zeta + \left(1 + {\zeta \over h} \right) \left[h_c \sigma + (h - h_c) C(\sigma)\right],

  \qquad \qquad -1 \leq \sigma \leq 0$$

where $h_c$ is either the minimum depth or a shallower depth above which we wish to have more resolution. $C(\sigma)$ is defined as:

$$C(\sigma) = (1 - b) {\sinh (\theta \sigma) \over \sinh \theta } +

  b { \tanh [\theta ( \sigma + {1\over 2})] -
  \tanh ( {1\over 2} \theta) \over 
  2 \tanh ( {1\over 2} \theta) }$$

where $\theta$ and $b$ are surface and bottom control parameters. Their ranges are $0 < \theta \leq 20$ and $0 \leq b \leq 1$, respectively. The first equation leads to $z = \zeta$ for $\sigma = 0$ and $z = h$ for $\sigma = -1$.

Some features of this coordinate system:

• It is a generalization of the traditional $\sigma$-coordinate system. Letting $\theta$ go to zero and using L'Hopital's rule, we get:

$$z = (\zeta + h)(1 + \sigma) - h$$

which is the traditional $\sigma$-coordinate.

• It is infinitely differentiable in $\sigma$.
• The larger the value of $\theta$, the more resolution is kept above $h_c$.
• For $b = 0$, the resolution all goes to the surface as $\theta$ is increased.
• For $b = 1$, the resolution goes to both the surface and the bottom equally as $\theta$ is increased.
• For $\theta \neq 0$ there is a subtle mismatch in the discretization of the model equations, for instance in the horizontal viscosity term. We recommend that you stick with "reasonable" values of $\theta$, say $\theta \leq 8$.
• Some problems turn out to be sensitive to the value of $\theta$ used.

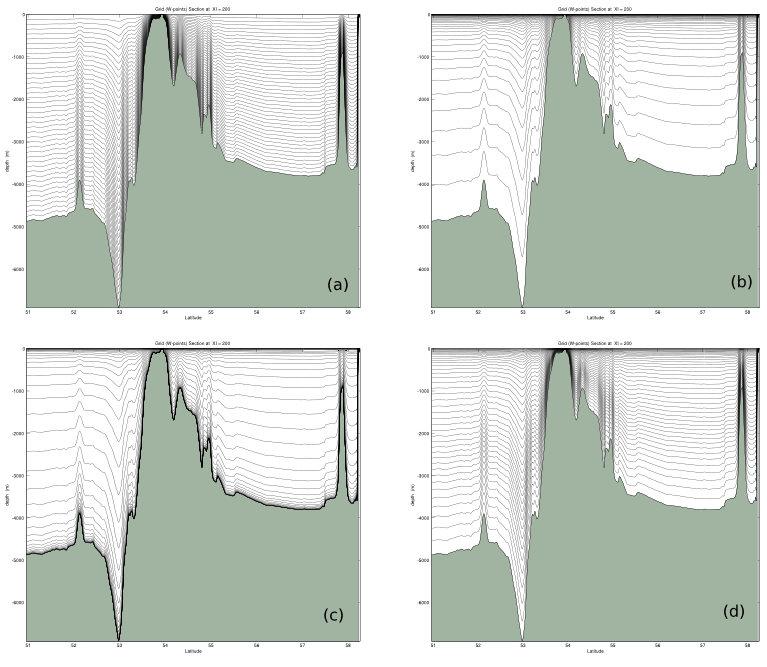
The following figure shows the $\sigma$-surfaces for several values of $\theta$ and $b$ for one of our domains. It was produced by a Matlab tool written by Hernan Arango which is available from our web site.

Figure: The $\sigma$-surfaces for the North Atlantic with (a) $\theta = 0.0001$ and $b = 0$, (b) $\theta = 8$ and $b = 0$, (c) $\theta = 8$ and $b = 1$. (d) The actual values used in this domain were $\theta = 5$ and $b = 0.4$.

We find it convenient to define: $$H_z \equiv {\partial z \over \partial \sigma}$$

The derivative of $C(\sigma)$ can be computed analytically:

$${\partial C(\sigma) \over \partial \sigma} = (1-b) {\cosh (\theta \sigma) \over

  \sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over
  2 \cosh^2 [ \theta (\sigma + {1\over 2})] } \theta$$

However, we choose to compute $H_z$ discretely as $\Delta z/ \Delta \sigma$ since this leads to the vertical sum of $H_z$ being exactly the total water depth $D$.

Note that though we have used this form of $\sigma$-coordinate, ROMS is written in such a way as to work with a variety of vertical mappings. There is one feature which is critical however. If the free surface is at rest, $\zeta = 0$, you get one solution for the level depths $z^{(0)}(k)$. In the case of nonzero $\zeta$, the displacements must be proportional to $\zeta$ and to the original distance from the bottom:

$$ z(k) = z^{(0)} (k) + \zeta \left( 1 + {z^{(0)} (k) \over h} \right) $$

or

$$ \Delta z(k) = \Delta z^{(0)} (k) \left( 1 + {\zeta \over h} \right) $$

This ensures that the vertical mass fluxes generated by a purely barotropic motion will vanish at every interface. </wikitex>