Parallelization
ROMS tiling
ROMS supports serial, OpenMP, and MPI computations, with the user choosing between them at compile time. The serial code can also take advantage of multiple small tiles which can be sized to fit in cache. All are accomplished through domain decomposition in the horizontal. All of the horizontal operations are explicit with a relatively small footprint, so the tiling is a logical choice. Some goals in the parallel design of ROMS were:
- Minimize code changes.
- Don't hard-code the number of processes.
- MPI and OpenMP share the same basic structure.
- Don't break the serial optimizations.
- Same result as serial code for any number of processes.
- Portability - able to run on any (Unix) system.
First, some C Preprocessor options. If we're compiling for MPI, the option -DMPI gets added to the argument list for cpp. Then, in globaldefs.h, we have:
# define DISTRIBUTE
#endif
The rest of the code uses DISTRIBUTE to identify distributed memory jobs. The OpenMP case is more straightforward, with -D_OPENMP getting passed to cpp and _OPENMP being the tag to check within ROMS.
The whole horizontal ROMS grid is shown here:
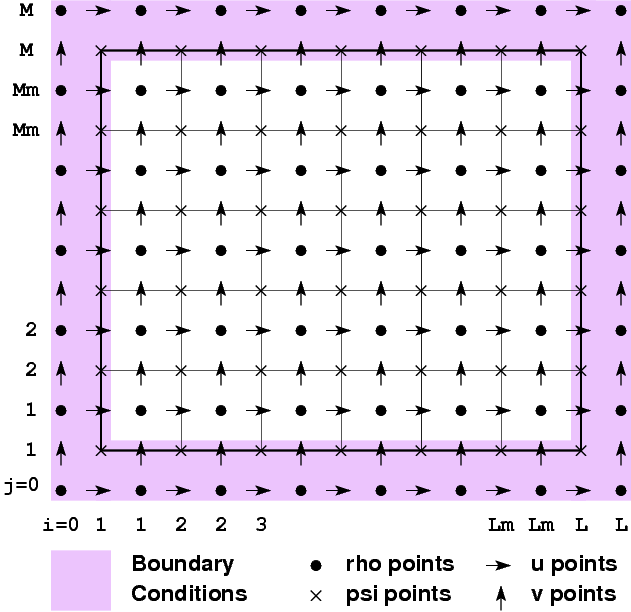
The computations are done over the cells inside the darker line; the cells are numbered 1 to Lm in the -direction and 1 to Mm in the -direction. Those looking ahead to running in parallel would be wise to include factors of two in their choice of Lm and Mm. ROMS will run in parallel with any values of Lm and Mm, but the computations might not be load-balanced.
ROMS internal numbers
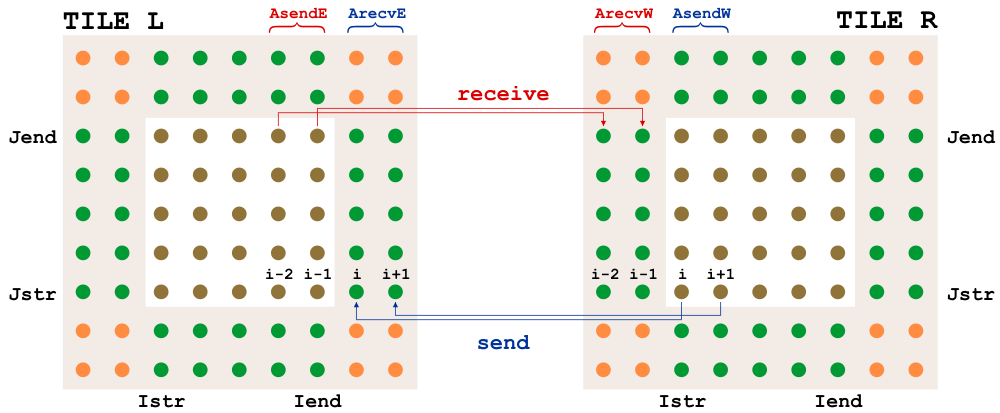
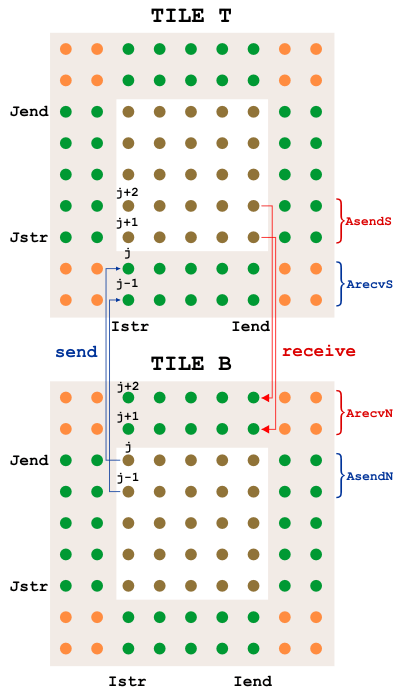
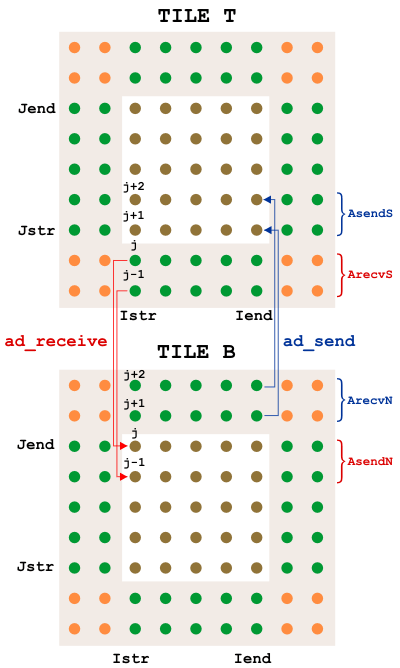
A domain with tiles is shown above, one color per tile. The overlap areas are known as ghost points or halo points. Each tile is an MPI process, an OpenMP thread, or a discrete unit of computation in a serial run. The tile contains enough information to time-step all the interior points, so the number of ghost points is dictated by the footprint of the algorithm using the largest number of neighbor points. In ROMS, the halo area would be two grids points wide unless the MPDATA advection scheme is used, in which case it needs three. The variable GHOST_POINTS is set accordingly:
# define GHOST_POINTS 3
# if defined DISTRIBUTE || defined EW_PERIODIC || defined NS_PERIODIC
# define THREE_GHOST
# endif
#else
# define GHOST_POINTS 2
#endif
The number of tiles is set in the input file as NtileI and NtileJ. For an MPI job, the product of the two must equal the number of MPI processes. For an OpenMP job, the number of threads must be a multiple of the number of tiles. For instance, for NtileI=4 and NtileJ=6, you must have 24 MPI processes while 2, 3, 4, 6, 8, 12 and 24 are all valid numbers of OpenMP threads. Also, a serial run could have 24 tiles and would just compute them sequentially.
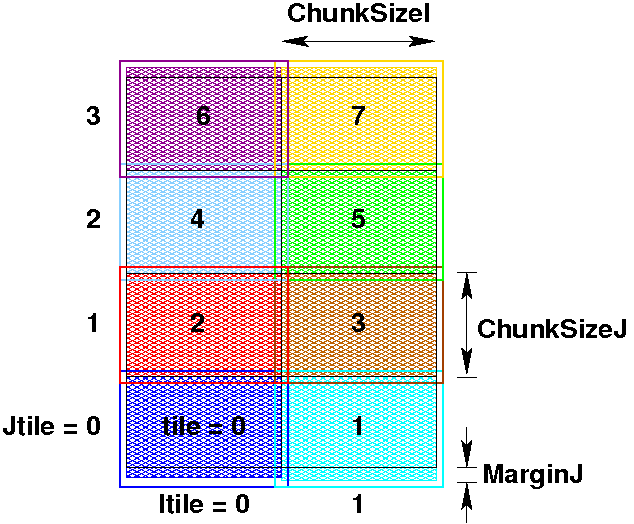
Once the input file has been read, we can compute the tile sizes:
ChunkSizeJ = (Mm+NtileJ-1)/NtileJ
MarginI = (NtileI*ChunkSizeI-Lm)/2
MarginJ = (NtileJ*ChunkSizeJ-Mm)/2
The internal ROMS numbers shown above are in the BOUNDS structure in mod_param.F. MarginI and MarginJ are zero if the numbers work out perfectly, i.e. Lm/NtileI and Mm/NtileJ are integers. The tile numbers match the MPI process numbers.
In picking a numbering scheme for indices within a tile, there are two common choices, as shown here:
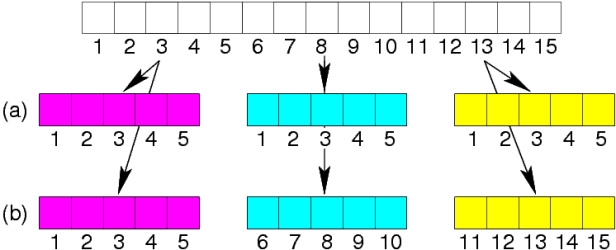
Each tile can be numbered from 1 to ChunksizeI or it can retain the numbering it would have in the whole grid. We have chosen this second option for ease when debugging features such as river inputs which apply to specific locations on the grid. It is simple to do using Fortran 90 dynamic memory allocation.
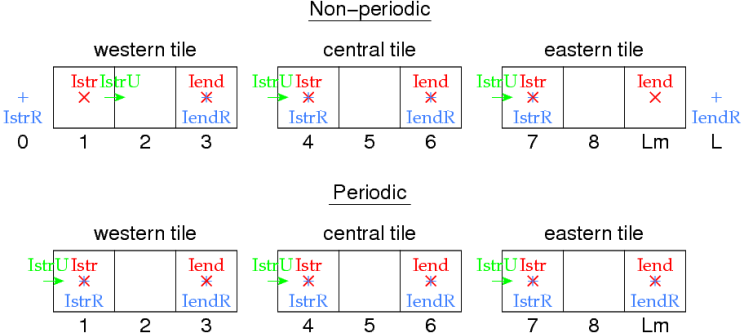
With the tile sizes known, we can assign beginning and ending indices for each tile. Some of the details depend on whether or not the domain is periodic in that direction, as shown here:
MPI exchange
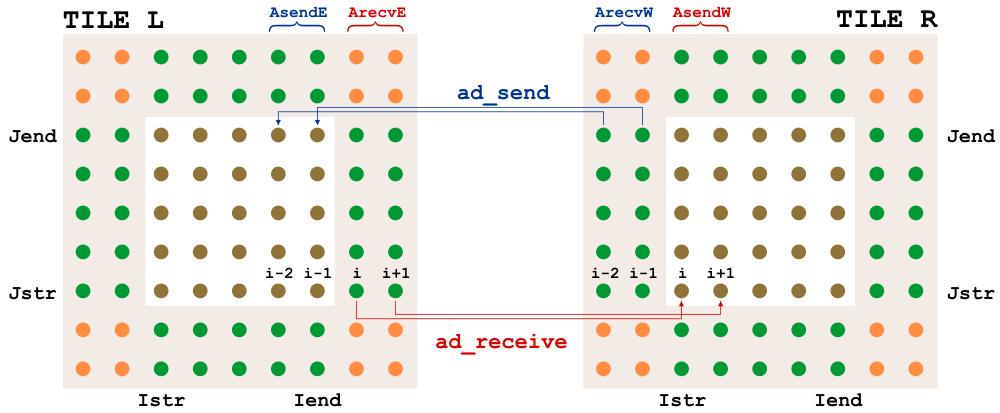
For MPI jobs, the ghost points need to be updated between interior point computations. The routines mp_exchange2d, mp_exchange3d and mp_exchange4d can be used to update the halo points of up to four arrays at a time. Each of these routines call tile_neighbors to figure out which tiles are neighboring and whether or not there really is a neighboring tile on each side. The mp_exchangexd routines then call:
mpi_send
mpi_wait
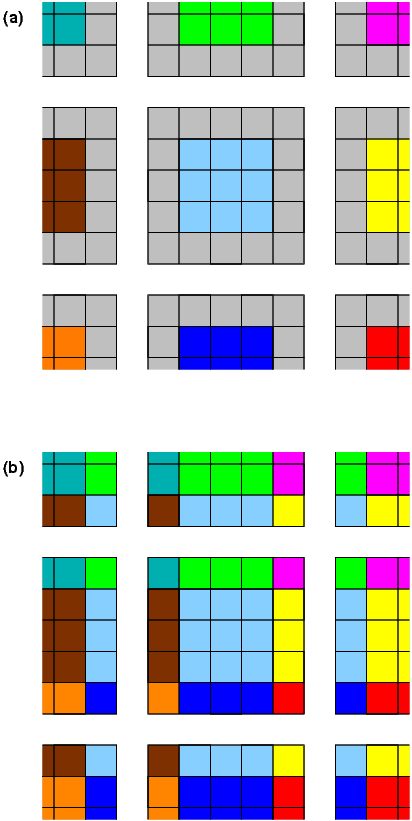
The exchanges happen first in the east-west direction, then in the north-south direction, saving the need for diagonal exchanges. A figure with interior points colored by tile and grey halo points needing an update is shown here, before and after an update:
Code syntax
In main3d.F, many function calls are surrounded by OpenMP parallel code such as:
DO thread=0,numthreads-1
subs=NtileX(ng)*NtileE(ng)/numthreads
DO tile=subs*thread,subs*(thread+1)-1,+1
CALL set_data (ng, TILE)
END DO
END DO
!$OMP END PARALLEL DO
What isn't obvious from this is that the argument TILE means different things depending on if we're using OpenMP or MPI:
# define TILE MyRank
#else
# define TILE tile
#endif
Likewise, NtileX also depends on whether or not we're using MPI:
NtileX(1:Ngrids)=1
#else
NtileX(1:Ngrids)=NtileI(1:Ngrids)
#endif
In other words, for MPI, TILE becomes the process number and the loop is only executed once.
In looking at a typical routine that's called from main3d, the routine is usually quite short, calling a _tile version of itself in which the actual work happens:
# include "tile.h"
CALL set_data_tile (ng, tile, &
& LBi, UBi, LBj, UBj, &
& IminS, ImaxS, JminS, JmaxS)
RETURN
END SUBROUTINE set_data
Here, there are two sets of array lower and upper bounds, those in the LBi family and those in the IminS family. Both depend on the Istr family shown in the figure above. The IminS family is for work arrays that are local to an MPI process or to an OpenMP thread, also local to a _tile routine. They are initialized:
ImaxS=BOUNDS(ng)%Iend(tile)+3
JminS=BOUNDS(ng)%Jstr(tile)-3
JmaxS=BOUNDS(ng)%Jend(tile)+3
and used:
real(r8), dimension(IminS:ImaxS,JminS:JmaxS) :: work2
The Istr and LBi families are dimensioned by the number of tiles once it is known by inp_par.F:
Ntiles=NtileI(ng)*NtileJ(ng)-1
allocate ( BOUNDS(ng) % LBi (-1:Ntiles) )
:
allocate ( BOUNDS(ng) % Jend (-1:Ntiles) )
END DO
They are then initialized in calls to the routines in get_bounds.F. If a tile is on the "western" edge (Itile=0), then UBi is set to LOWER_BOUND_I.
:
IF ((Itile.eq.-1).or.(Itile.eq.0)) THEN
LBi=Imin
ELSE
LBi=Istr-Nghost
END IF
Tracking the origins of LOWER_BOUND_I, we find it in globaldefs.h:
# define LOWER_BOUND_I -GHOST_POINTS
#else
# define LOWER_BOUND_I 0
#endif
In the case of set_data, we are simply passing array indices for the tiled arrays. To access the tiled arrays from within set_data_tile, we need to use the relevant modules and then refer to the array with its full name:
:
CALL set_2dfld_tile (ng, tile, iNLM, idCfra, &
& LBi, UBi, LBj, UBj, &
& FORCES(ng)%cloudG, &
& FORCES(ng)%cloud, &
& update)
In other cases, the parent routine would have the use, then would pass the relevant array to the _tile routine:
:
CALL prsgrd_tile (ng, tile, &
:
& GRID(ng) % Hz, &
:
SUBROUTINE prsgrd_tile (ng, tile, &
:
& Hz, z_r, z_w, &
:
real(r8), intent(in) :: Hz(LBi:,LBj:,:)
This allows the _tile routine to use Hz with the same syntax as the pre-parallel, pre-module code once had.
Input/output
In ROMS, the distributed memory I/O is all happening on the master process (0) unless you specifically ask it to use MPI-I/O, which requires both the NETCDF4 and PARALLEL_IO cpp flags to be defined. If you do this, you will be reading and writing HDF5 files and will need to update your pre- and post-processing tools accordingly. I have tentatively tried the parallel I/O and found it to be exceedingly slow - I've been told since that this is the fault of the NetCDF-4 layer sitting on top of HDF5 - HDF5 alone should be fast.
In the case of having all the I/O pass through the master process, we can still read and write classic NetCDF-3 files. Care must be taken though, in the event of an error. ROMS has been cleaned up so that the master process will broadcast its return state to the other processes and they can all die gracefully together when there is a problem.
An example of a routine which reads from disk is get_grid, called from initial. Each MPI process calls get_grid:
# ifdef DISTRIBUTE
CALL mp_bcasti (ng, iNLM, exit_flag)
# endif
if (exit_flag.ne.NoError) RETURN
If any one of the processes has trouble, it will enter into the exit_flag which is then shared by all.
To read in an array variable, all processes in get_grid uses nf_fread2d and friends:
& var_name(it), var_id(it), &
& 0, gtype, Vsize, &
& LBi, UBi, LBj, UBj, &
& Fscl, Fmin, Fmax, &
& GRID(ng) % rmask, &
& GRID(ng) % rmask)
IF (status.ne.nf90_noerr) THEN
exit_flag=2
ioerror=status
EXIT
END IF
Within nf_fread2d, we get to a call to the NetCDF library from just the master process:
status=nf90_get_var(ncid, ncvarid, wrk, start, total)
:
END IF
# ifdef DISTRIBUTE
CALL mp_bcasti (ng, model, status)
# endif
IF (status.ne.nf90_noerr) THEN
exit_flag=2
ioerror=status
nf_fread2d=status
RETURN
END IF
At this point, the master process has the entire 2-D array stored in wrk. This then needs to be divvied out to the various tiles to their copy of the array in question (stored in the A argument to nf_fread2d):
CALL mp_scatter2d (ng, model, LBi, UBi, LBj, UBj, &
& Nghost, MyType, Amin, Amax, &
# if defined READ_WATER && defined MASKING
& NWpts, SCALARS(ng)%IJwater(:,wtype), &
# endif
& Npts, wrk, A)
Something similar happens when writing to output files.
Other figures