Home
Explorer of the Seas
Introduction
Institutions
Data
Observations
About the Model
Data Assimilation
Assimilation Products
Assimilation Impact
Ensemble Archives
References
Acknowledgements

Data Assimilation

The data assimilaton approach used is a incremental 4-Dimensional Variational (IS4DVAR) method. IS4DVAR seeks to minimize the cost function J given by:



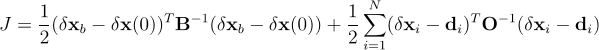
where x denotes the ROMS state-vector (T, S, u, v, ζ), and δx denotes increments about a background or first-guess solution denoted x_b; d_i = y_i - Hx_i is the observation increment at time i, where y_i are the observed values of x_i and H (the observation operator) maps x_i to the observation points; and B and O are the background and observations error covariance matrices respectively.

The gradient ∂J/∂x(0) with respect to variations in the model initial conditions can be computed by running the adjoint of ROMS forced by the innovations O^-1(δx_i - d_i). A preconditioned conjugate gradient method uses the gradient information to adjust x(0) so that J decreases during the next integration of ROMS. An iterative algorithm is used to minimize J and utilizes ROMS, the tangent linear version of ROMS, and the adjoint of ROMS. The background error covariance matrix B is modeled as a diffusion operator, and the conjugate gradient algorithm is preconditioned by B^1/2 following Weaver and Courtier (2001). The ROMS IS4DVAR system follows closely similar approaches described by Weaver et al (2003) and Vialard et al (2003).