Difference between revisions of "Vertical S-coordinate"
(Added s-coordinate figure) (change visibility) |
(convert to TeX) (change visibility) |
||
| Line 1: | Line 1: | ||
<div class="title">S-coordinate</div> | <div class="title">S-coordinate</div> | ||
<wikitex> | |||
Following Song and Haidvogel (1994), the vertical coordinate has | Following Song and Haidvogel (1994), the vertical coordinate has | ||
been chosen to be: | been chosen to be: | ||
$$z = \zeta + \left(1 + {\zeta \over h} \right) \left[h_c s + (h - h_c) C(s)\right], | |||
\qquad \qquad -1 \leq s \leq 0 | \qquad \qquad -1 \leq s \leq 0$$ | ||
where | where $h_c$ is either the minimum depth or a shallower depth above which we wish to have more resolution. $C(s)$ is defined as: | ||
$$C(s) = (1 - b) {\sinh (\theta s) \over \sinh \theta } + | |||
b { \tanh [\theta ( s + {1\over 2})] - | b { \tanh [\theta ( s + {1\over 2})] - | ||
\tanh ( {1\over 2} \theta) \over | \tanh ( {1\over 2} \theta) \over | ||
2 \tanh ( {1\over 2} \theta) } | 2 \tanh ( {1\over 2} \theta) }$$ | ||
where | where $\theta$ and $b$ are surface and bottom control parameters. Their ranges are $0 < \theta \leq 20$ and $0 \leq b \leq 1$, respectively. The first equation leads to $z = \zeta$ for $s = 0$ and $z = h$ for $s = -1$. | ||
respectively. The first equation leads to | |||
Some features of this coordinate system: | Some features of this coordinate system: | ||
*It is a generalization of the | *It is a generalization of the $\sigma$-coordinate system. Letting $\theta$ go to zero and using L'Hopital's rule, we get: | ||
$$z = (\zeta + h)(1 + s) - h$$ | |||
which is the | which is the $\sigma$-coordinate. | ||
* It has a linear dependence on | * It has a linear dependence on $\zeta$ and is infinitely differentiable in $s$. | ||
* The larger the value of | * The larger the value of $\theta$, the more resolution is kept above $h_c$. | ||
* For | * For $b = 0$, the resolution all goes to the surface as $\theta$ is increased. | ||
* For | * For $b = 1$, the resolution goes to both the surface and the bottom equally as $\theta$ is increased. | ||
* For | * For $\theta \neq 0$ there is a subtle mismatch in the discretization of the model equations, for instance in the horizontal viscosity term. We recommend that you stick with "reasonable" values of $\theta$, say $\theta \leq 5$. | ||
* Some problems turn out to be sensitive to the value of | * Some problems turn out to be sensitive to the value of $\theta$ used. | ||
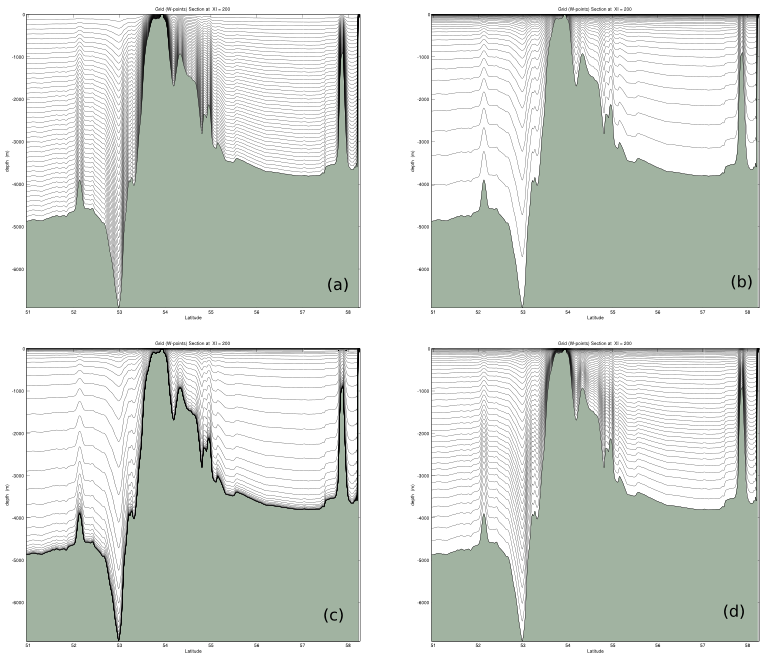
The following figure shows the | The following figure shows the $s$-surfaces for several values of $\theta$ and $b$ for one of our domains. It was produced by a Matlab tool written by Hernan Arango which is available from our web site. | ||
written by Hernan Arango which is available from our web site. | |||
[[Image:Scoord.png|vertical s-coordinate]] | [[Image:Scoord.png|vertical s-coordinate]] | ||
Figure: The | Figure: The $s$-surfaces for the North Atlantic with (a) $\theta = 0.0001$ and $b = 0$, (b) $\theta = 8$ and $b = 0$, (c) $\theta = 8$ and $b = 1$. (d) The actual values used in this domain were $\theta = 5$ and $b = 0.4$. | ||
We find it convenient to define: | We find it convenient to define: | ||
$$H_z \equiv {\partial z \over \partial s}$$ | |||
The derivative of | The derivative of $C(s)$ can be computed analytically: | ||
$${\partial C(s) \over \partial s} = (1-b) {\cosh (\theta s) \over | |||
\sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over | \sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over | ||
2 \cosh^2 [ \theta (s + {1\over 2})] } \theta | 2 \cosh^2 [ \theta (s + {1\over 2})] } \theta$$ | ||
However, we choose to compute | However, we choose to compute $H_z$ discretely as $\Delta z/ \Delta s$ since this leads to the vertical sum of $H_z$ being exactly the total water depth $D$. | ||
</wikitex> | |||
Revision as of 18:53, 10 July 2008
<wikitex> Following Song and Haidvogel (1994), the vertical coordinate has been chosen to be:
$$z = \zeta + \left(1 + {\zeta \over h} \right) \left[h_c s + (h - h_c) C(s)\right],
\qquad \qquad -1 \leq s \leq 0$$
where $h_c$ is either the minimum depth or a shallower depth above which we wish to have more resolution. $C(s)$ is defined as:
$$C(s) = (1 - b) {\sinh (\theta s) \over \sinh \theta } +
b { \tanh [\theta ( s + {1\over 2})] -
\tanh ( {1\over 2} \theta) \over
2 \tanh ( {1\over 2} \theta) }$$
where $\theta$ and $b$ are surface and bottom control parameters. Their ranges are $0 < \theta \leq 20$ and $0 \leq b \leq 1$, respectively. The first equation leads to $z = \zeta$ for $s = 0$ and $z = h$ for $s = -1$.
Some features of this coordinate system:
- It is a generalization of the $\sigma$-coordinate system. Letting $\theta$ go to zero and using L'Hopital's rule, we get:
$$z = (\zeta + h)(1 + s) - h$$
which is the $\sigma$-coordinate.
- It has a linear dependence on $\zeta$ and is infinitely differentiable in $s$.
- The larger the value of $\theta$, the more resolution is kept above $h_c$.
- For $b = 0$, the resolution all goes to the surface as $\theta$ is increased.
- For $b = 1$, the resolution goes to both the surface and the bottom equally as $\theta$ is increased.
- For $\theta \neq 0$ there is a subtle mismatch in the discretization of the model equations, for instance in the horizontal viscosity term. We recommend that you stick with "reasonable" values of $\theta$, say $\theta \leq 5$.
- Some problems turn out to be sensitive to the value of $\theta$ used.
The following figure shows the $s$-surfaces for several values of $\theta$ and $b$ for one of our domains. It was produced by a Matlab tool written by Hernan Arango which is available from our web site.
Figure: The $s$-surfaces for the North Atlantic with (a) $\theta = 0.0001$ and $b = 0$, (b) $\theta = 8$ and $b = 0$, (c) $\theta = 8$ and $b = 1$. (d) The actual values used in this domain were $\theta = 5$ and $b = 0.4$.
We find it convenient to define: $$H_z \equiv {\partial z \over \partial s}$$
The derivative of $C(s)$ can be computed analytically:
$${\partial C(s) \over \partial s} = (1-b) {\cosh (\theta s) \over
\sinh \theta} \theta + b {\coth ( {1 \over 2} \theta) \over
2 \cosh^2 [ \theta (s + {1\over 2})] } \theta$$
However, we choose to compute $H_z$ discretely as $\Delta z/ \Delta s$ since this leads to the vertical sum of $H_z$ being exactly the total water depth $D$. </wikitex>