Difference between revisions of "Regional Ocean Modeling System (ROMS)"

From WikiROMS
Jump to navigationJump to search
 
(46 intermediate revisions by 2 users not shown)
Line 1: Line 1:
<div class="title">Introduction</div>
<div class="title">ROMS History</div>
ROMS is a free-surface, terrain-following, primitive equations ocean model widely used by the scientific community for a diverse range of applications (''e.g.'', [[Bibliography#HaidvogelDB_2000a | Haidvogel et al., 2000]]; [[Bibliography#MarchesielloP_2003a | Marchesiello et al., 2003]]; [[Bibliography#PelizA_2003a | Peliz et al., 2003]]; [[Bibliography#DiLorenzoE_2003a | Di Lorenzo, 2003]]; [[Bibliography#DinnimanMS_2003a | Dinniman et al., 2003]]; [[Bibliography#BudgellWP_2005a | Budgell, 2005]]; [[Bibliography#WarnerJC_2005a | Warner et al., 2005a]], [[Bibliography#WarnerJC_2005b | b]]; [[Bibliography#WilkinJL_2005a | Wilkin et al., 2005]]).
In the fall of 1995, Hernan G. Arango (hereafter <span class="blue">HGA</span>) started working at the Ocean Modeling Lab ('''OML'''), Institute of Marine and Coastal Sciences ('''IMCS'''), Rutgers University. His first assignment from '''OML''''s group leader Dale B. Haigvogel (hereafter <span class="blue">DBH</span>) was to work on the classic baroclinic, wind-driven, double gyre problem with the now-extinct '''S'''-'''C'''oordinate '''R'''utgers '''U'''niversity '''M'''odel ('''SCRUM''', Song and Haidvogel, 1994), which was derived from '''SPEM''' ('''S'''emi-spectral '''P'''rimitive '''E'''quation '''M'''odel; Haidvogel ''et al.'', 1991). The double-gyre application is affectionately known as '''Big Bad Basin''' (nowadays, <span class="mediumOrchid">BASIN</span> test case) by several '''OML''' modelers because of its stability issues in long simulations. After a couple of months of struggling with the <span class="mediumOrchid">BASIN</span> problem, <span class="blue">HGA</span> decided to rewrite '''SCRUM''' from scratch and modify its numerical kernel, including time-stepping, advection schemes, and implementing a split-explicit treatment coupling between barotropic (fast) and barotropic (slow) governing equations in collaboration with '''OML''''s scientists Robert J. Chant and Katherine S. Hedström. In addition, a complete overhaul of the model metadata, input, and output files with NetCDF format. And voilà, the <span class="mediumOrchid">BASIN</span> application ran successfully for several years. The new model became '''SCRUM''' version '''3.0''', which later evolved to '''SCRUM 4.0''' and then becomes the '''R'''egional '''O'''cean '''M'''odeling '''S'''ystem ('''ROMS'''). The acronym '''ROMS''' was inspired by the '''R'''egional '''A'''tmospheric '''M'''odeling '''S'''ystem ('''RAMS'''). Thus, at the time, there was a regional numerical model for the atmosphere and ocean with similar acronyms.
The algorithms that comprise ROMS computational nonlinear kernel are described in detail in Shchepetkin and McWilliams ([[Bibliography#ShchepetkinAF_2003a | 2003]], [[Bibliography#ShchepetkinAF_2005a | 2005]]), and the tangent linear and adjoint kernels and platforms are described in [[Bibliography#MooreAM_2004a | Moore et al. (2004)]].
ROMS includes accurate and efficient physical and numerical algorithms and several coupled models for biogeochemical ([[Bibliography#PowellTP_2006a |Power et al., 2006]]; [[Bibliography#FennelK_2006a |Fennel et al., 2006]]), bio-optical ([[Bibliography#BissettWP_1999a |Bissett et al., 1999]]), sediment ([[Bibliography#WarnerJC_2006a |Warner et al., 2006]]), and sea ice ([[Bibliography#BudgellWP_2005a |Budgell, 2005]]) applications.
It also includes several vertical mixing schemes ([[Bibliography#WarnerJC_2005a |Warner et al., 2005a]]), multiple levels of nesting and composed grids.


For computational economy, the hydrostatic primitive equations for momentum are solved using a split-explicit time-stepping scheme which requires special treatment and coupling between barotropic (fast) and baroclinic (slow) modes. A finite number of barotropic time steps, within each baroclinic step, are carried out to evolve the free-surface and vertically integrated momentum equations. In order to avoid the errors associated with the aliasing of frequencies resolved by the barotropic steps but unresolved by the baroclinic step, the barotropic fields are time averaged before they replace those values obtained with a longer baroclinic step. A cosine-shape time filter, centered at the new time level, is used for the averaging of the barotropic fields ([[Bibliography#ShchepetkinAF_2005a |Shchepetkin and McWilliams, 2005]]). In addition, the separated time-stepping is constrained to maintain exactly both volume conservation and consistancy preservation properties which are needed for the tracer equations ([[Bibliography#ShchepetkinAF_2005a |Shchepetkin and McWilliams, 2005]]). Currently, all 2D and 3D equations are time-discretized using a third-order accurate predictor (Leap-Frog) and corrector (Adams-Molton) time-stepping algorithm which is very robust and stable. The enhanced stability of the scheme allows larger time steps, by a factor of about four, which more than offsets the increased cost of the predictor-corrector algorithm.
In 1998, James C. McWilliams (hereafter, <span class="blue">JCM</span>) started looking for a regional ocean model for the U.S. West Coast and contacted <span class="blue">DBH</span> for possible collaborations. As a result, <span class="blue">DBH</span> and <span class="blue">HGA</span> traveled to Los Angeles, to meet at University of California, Los Angeles (UCLA) with <span class="blue">JCM</span> and Alexander F. Shchepetkin  (hereafter <span class="blue">AFS</span>) or just Sasha, as the '''ROMS''' VIPs know him. The expectation that <span class="blue">HGA</span> and <span class="blue">AFS</span> would get along was very low. However, their mutual respect, skills, and friendship grew. As a result, and to the benefit of the ocean modeling community,  '''ROMS''' was officially born. Their first task was to improve its efficiency by implementing a multi-threaded parallel version of its numerical kernel using the shared-memory paradigm native to the IRIX operating system available on SGI supercomputers of the time. The shared-memory compiling directives evolved later to the portable '''OpenMP''' standard implementation in '''ROMS'''. Moreover, <span class="blue">AFS</span> began looking at the ensemble code and started counting operations; multiplications replaced unnecessary divisions when appropriate, and '''DO'''-loops were reorganized and pipelined to reduce memory hits. <span class="blue">HGA</span> learned how to count operations and analyzed optimized Fortran code, which was available at the time, to minimize the need for automatic optimization. As a result, the '''ROMS''' code was very efficient and fast. Nowadays, '''ROMS''' can be compiled with aggressive Fortran optimization flags. Of course, users need to be aware that the bold optimization flags in some compilers could compromise the numerical '''IEEE''' floating-point precision, and new flags are required to retain it, which may slow down the computations.


In the vertical, the primitive equations are discretized over variable topography using stretched terrain-following coordinates ([[Bibliography#SongY_1994a |Song and Haidvogel, 1994]]). The stretched coordinates allow increased resolution in areas of interest, such as thermocline and bottom boundary layers. The default stencil uses centered, second-order finite differences on a staggered vertical grid. Options for higher order stencil are available via a conservative, parabolic spline reconstruction of vertical derivatives ([[Bibliography#ShchepetkinAF_2005a |Shchepetkin and McWilliams, 2005]]). This class of model exhibits stronger sensitivity to topography which results in pressure gradient errors. These errors arise due to splitting of the pressure gradient term into an along-sigma component and a hydrostatic correction (for details, see [[Bibliography#HaidvogelDB_1999a | Haidvogel and Beckmann, 1999]]). The numerical algorithm in ROMS is designed to reduce such errors ([[Bibliography#ShchepetkinAF_2003a |Shchepetkin and McWilliams, 2003]]).
In 2000, Terri Paluszkiewicz from the Office of Naval Research (ONR) approached <span class="blue">HGA</span> and <span class="blue">JCM</span> about funding opportunities to develop the next generation of a regional, high-resolution ocean model with accurate numerical algorithms and data assimilation capabilities. As a result, ONR started funding '''ROMS''' development separately to Rutgers (data assimilation and adjoint-based algorithms, applications, maintenance, and community outreach) and UCLA (numerical algorithms and applications). Then, <span class="blue">HGA</span> suggested to ONR that a redesign of '''ROMS''' was required, and a team of experts was needed to do variational data assimilation correctly. During his years at Harvard, <span class="blue">HGA</span> had the opportunity to meet Andrew M. Moore (hereafter, <span class="blue">AMM</span>), now at the University of California, Santa Cruz (UCSC), and work with Arthur J. Miller (hereafter, <span class="blue">AJM</span>) from the Scripps Institute of Oceanography (SIO). <span class="blue">AMM</span> is an expert on adjoint-based modeling and applications. Therefore, the <span class="blue">ROMS</span> data assimilation team included <span class="blue">AMM</span>, <span class="blue">HGA</span>, <span class="blue">AJM</span>, collaborator Bruce D. Cornuelle (hereafter, <span class="blue">BDC</span>), and Ph. D. student Emanuele Di Lorenzo (hereafter, <span class="blue">EDL</span>), and Douglas J. Neilson (Hereafter, <span class="blue">DJW</span>). ONR also funded UCSC and SIO separately for this work. Thus, it started a very successful collaboration with several peer-reviewed publications in journals and books. The chemistry between the '''ROMS''' Data Assimilation ('''ROMS-DA''') group was extraordinary, with lots of fun, good food, and great wine-tasting parties.


In the horizontal, the primitive equations are evaluated using boundary-fitted, orthogonal curvilinear coordinates on a staggered Arakawa C-grid. The general formulation of curvilinear coordinates includes both Cartesian (constant metrics) and spherical (variable metrics) coordinates. Coastal boundaries can also be specified as a finite-discretized grid via land/sea masking. As in the vertical, the horizontal stencil utilizes a centered, second-order finite differences. However, the code is designed to make the implementation of higher order stencils easily.
[[Image:AdjointGroup.jpg|1000px|center]]
<center>'''''ROMS Adjoint Group:''''' Back, left to right: Arthur J. Miller, Andrew M. Moore, Bruce D. Cornuelle, and Douglas J. Neilson. Front: Hernan G. Arango and Emanuel Di Lorenzo. </center>


ROMS has various options for advection schemes: second- and forth-order centered differences; and third-order, upstream biased. The later scheme is the model default and it has a velocity-dependent hyper-diffusion dissipation as the dominant truncation error ([[Bibliography#ShchepetkinAF_1998a |Shchepetkin and McWilliams, 1998]]). These schemes are stable for the predictor-corrector methodology of the model. In addition, there is an option for conservative parabolic spline representation of vertical advection which has dispersion properties similar to an eight-order accurate conventional scheme.
<span class="blue">AMM</span> and <span class="blue">HGA</span> frequently traveled to Scripps, in La Jolla, for an intense week-long perturbation, tangent linear model ('''TLM''') and adjoint model ('''ADM''') code writing. <span class="blue">AMM</span> was the master teaching and directing the monkies on how to write '''ROMS-TL''' and '''ROMS-AD''' codes. The '''TLM''' and '''ADM''' were hand-coded from the discrete nonlinear ('''NLM''') code using the recipes of Giering and Kaminski (1998). Therefore, any change to its dynamical and numerical kernels will affect the symmetry of the '''TLM''' and '''ADM''' operators. Moreover, the resulting discrete adjoint is exact and is defined relative to the inner product that prescribes the '''L2'''-norm. The finite-amplitude, tangent linear code for the Representer model ('''RPM''') was later derived from the '''TLM'''. The '''RPM''' is used in the indirect, representer-based approach for 4-Dimensional Variational ('''4D-Var''') data assimilation.


There are several subgrid-scale parameterizations in ROMS. The horizontal mixing of momentum and tracers can be along vertical levels, geopotential (constant depth) surfaces, or isopycnic (constant density) surfaces. The mixing operator can be harmonic (3-point stencil) or biharmonic (5-point stencil). See [[Bibliography#HaidvogelDB_1999a | Haidvogel and Beckmann (1999)]] for an overview of all these operators.
To be continued ...


The vertical mixing parameterization in ROMS can be either by local or nonlocal closure schemes. The local closure schemes are based on the level 2.5 turbulent kinetic energy equations by [[Bibliography#MellorGL_1982a | Mellor and Yamada (1982)]] and the [[Generic Length Scale]] (GLS) parameterization ([[Bibliography#UmlaufL_2003a |Umlauf and Burchard, 2003]]). The nonlocal closure scheme is based on the K-profile, boundary layer formulation by [[Bibliography#LargeWG_1994a | Large et al. (1994)]]. The K-profile scheme has been expanded to include both surface and bottom oceanic boundary layers. The GLS is a two-equation turbulence model that allows a wide range of vertical mixing closures, including the popular k-kl (Mellor-Yamada level 2.5), k-e, and k-w schemes. Several stability functions ([[Bibliography#GalperinB_1988a |Galperin et al., 1988]]; [[Bibliography#KanthaLH_1994a | Kantha and Clayson, 1994]]; [[Bibliography#CanutoVM_2001a | Canuto et al., 2001]]) have been also added to provide further flexibility. A recent study ([[Bibliography#WarnerJC_2005a |Warner et al., 2005a]]) evaluated the performance of these turbulence closures in ROMS in terms of idealized sediment transport applications. In addition, there is a wave/current bed boundary layer scheme that provides the bottom stress ([[Bibliography#StylesR_2000a |Styles and Glenn, 2000]]) and sediment transport which become important in coastal applications.
===ROMS Releases===


Currently, the air-sea interaction boundary layer in ROMS is based on the bulk parameterization of [[Bibliography#FairallCW_1996a | Fairall et al. (1996)]]. It was adapted from the COARE (Coupled Ocean-Atmosphere Response Experiment) algorithm for the computation of surface fluxes of momentum, sensible heat, and latent heat. This boundary layer is used for one or two-way coupling with atmospheric models.
The following table shows information about the infrequent tagged '''ROMS''' releases showing its evolution and expansion. It was redesigned completely starting with version '''ROMS 2.0''' and written in '''Fortran-1990''' standard with modules with the '''derived-type''' objects with '''dynamical allocation''', and managed with '''svn''' repositories instead of '''cvs'''. Some features of '''Fortran-1995''' and '''Fortran-2003''' standards were introduced later when available in mostly all compilers. The perturbation Tangent Linear Model ('''TLM'''), finite-amplitude Tangent Linear (Representer) Model ('''RPM'''), and adjoint model ('''ADM''') were released in version '''ROMS 2.3'''.  


ROMS is a very modern code and uses C-preprocessing to activate the various physical and numerical options. The code can be run in either serial or parallel computers. The code uses a coarse-grained parallelization paradigm which partitions the computational 3D grid into tiles. Each tile is then operated on by different parallel threads. Originally, the code was designed for shared-memory computer architectures and the parallel compiler-dependent directives (OpenMP Standard) are placed only in the main computational routine of the code. An MPI version of the code has been developed so both shared and distributed-memory paradigms coexist together in a single code.


ROMS is a very modern and modular code written in F90/F95. It uses C-preprocessing to activate the various physical and numerical options. Several coding standards have been established to facilitate model readability, maintenance, and portability. All the state model variables are dynamically allocated and passed as arguments to the computational routines via de-referenced pointer structures. All private or scratch arrays are automatic; their size is determined when the procedure is entered. This code structure facilitates computations over nested and composed grids. The parallel framework is coarse-grained with both shared- and distributed-memory paradigms coexisting in the same code. The shared-memory option follows OpenMP 2.0 standard. ROMS has a generic distributed-memory interface that facilitates the use of several message passage protocols. Currently, the data exchange between nodes is done with MPI. However, other protocols like MPI2, SHMEM, and others can be coded without much effort.
:{| border="1" cellspacing="0" cellpadding="5" align="left"
| align="center" | <span class="violet">Tag Version</span>
| align="center" | <span class="violet">svn Revision</span>
| align="center" | <span class="violet">Release Date</span>
| align="center" | <span class="violet">Number of Files</span>
| align="center" | <span class="violet">Lines of Code</span>
|-
| align="center" | '''1.1.0'''
| align="center" | '''cvs -r 1.1.0'''
| align="center" | '''1999-01-20'''
| align="center" | '''125'''
| align="center" | '''44,639'''
|-
| align="center" | '''1.2.0'''
| align="center" | '''cvs -r 1.2.0'''
| align="center" | '''1999-01-25'''
| align="center" | '''130'''
| align="center" | '''46,905'''
|-
| align="center" | '''1.3.0'''
| align="center" | '''cvs -r 1.3.0'''
| align="center" | '''1999-03-15'''
| align="center" | '''131'''
| align="center" | '''47,931'''
|-
| align="center" | '''1.4.0'''
| align="center" | '''cvs -r 1.4.0'''
| align="center" | '''1999-06-20'''
| align="center" | '''146'''
| align="center" | '''49,466'''
|-
| align="center" | '''1.5.0'''
| align="center" | '''cvs -r 1.5.0'''
| align="center" | '''2000-02-10'''
| align="center" | '''145'''
| align="center" | '''56,118'''
|-
| align="center" | '''1.6.0'''
| align="center" | '''cvs -r 1.6.0'''
| align="center" | '''2000-01-29'''
| align="center" | '''144'''
| align="center" | '''56,066'''
|-
| align="center" | '''1.6.1'''
| align="center" | '''cvs -r 1.6.1'''
| align="center" | '''2000-03-06'''
| align="center" | '''144'''
| align="center" | '''56,123'''
|-
| align="center" | '''1.6.2'''
| align="center" | '''cvs -r 1.6.2'''
| align="center" | '''2000-03-17'''
| align="center" | '''144'''
| align="center" | '''56,283'''
|-
| align="center" | '''1.7.0'''
| align="center" | '''cvs -r 1.7.0'''
| align="center" | '''2001-01-19'''
| align="center" | '''165'''
| align="center" | '''63,652'''
|-
| align="center" | '''1.7.1'''
| align="center" | '''cvs -r 1.7.1'''
| align="center" | '''2001-02-01'''
| align="center" | '''165'''
| align="center" | '''63,573'''
|-
| align="center" | '''1.7.2'''
| align="center" | '''cvs -r 1.7.2'''
| align="center" | '''2001-04-17'''
| align="center" | '''173'''
| align="center" | '''66,324'''
|-
| align="center" | '''1.8.0'''
| align="center" | '''cvs -r 1.8.0'''
| align="center" | '''2002-01-11'''
| align="center" | '''175'''
| align="center" | '''67,999'''
|- style="background-color: #D0FFD0;"
| align="center" | '''2.0'''
| align="center" | '''2'''
| align="center" | '''2003-06-30'''
| align="center" | '''232'''
| align="center" | '''95,836'''
|-
| align="center" | '''2.1'''
| align="center" | '''3'''
| align="center" | '''2004-05-05'''
| align="center" | '''253'''
| align="center" | '''117,956'''
|-
| align="center" | '''2.2'''
| align="center" | '''4'''
| align="center" | '''2005-05-26'''
| align="center" | '''297'''
| align="center" | '''158,176'''
|-
| align="center" | '''2.3'''
| align="center" | '''8'''
| align="center" | '''2007-02-06'''
| align="center" | '''1,122'''
| align="center" | '''399,457'''
|-
| align="center" | '''3.0'''
| align="center" | '''36'''
| align="center" | '''2007-04-27'''
| align="center" | '''1,313'''
| align="center" | '''460,643'''
|-
| align="center" | '''3.1'''
| align="center" | '''166'''
| align="center" | '''2008-03-17'''
| align="center" | '''1,345'''
| align="center" | '''470,110'''
|-
| align="center" | '''3.2'''
| align="center" | '''338'''
| align="center" | '''2009-03-25'''
| align="center" | '''1,428'''
| align="center" | '''549,318'''
|-
| align="center" | '''3.3'''
| align="center" | '''432'''
| align="center" | '''2009-12-26'''
| align="center" | '''1,559'''
| align="center" | '''603,578'''
|-
| align="center" | '''3.4'''
| align="center" | '''550'''
| align="center" | '''2011-04-19'''
| align="center" | '''1,583'''
| align="center" | '''643,878'''
|-
| align="center" | '''3.5'''
| align="center" | '''568'''
| align="center" | '''2011-09-21'''
| align="center" | '''1,582'''
| align="center" | '''648,098'''
|-
| align="center" | '''3.6'''
| align="center" | '''656'''
| align="center" | '''2013-04-18'''
| align="center" | '''1,638'''
| align="center" | '''684,351'''
|-
| align="center" | '''3.7'''
| align="center" | '''974'''
| align="center" | '''2019-07-25'''
| align="center" | '''1,784'''
| align="center" | '''844,948'''
|-
| align="center" | '''3.8'''
| align="center" | '''995'''
| align="center" | '''2020-01-09'''
| align="center" | '''1,799'''
| align="center" | '''848,245'''
|-
| align="center" | '''3.9'''
| align="center" | '''1054'''
| align="center" | '''2021-03-06'''
| align="center" | '''1,909'''
| align="center" | '''884,508'''
|-
| align="center" | '''4.0'''
| align="center" | '''1108'''
| align="center" | '''2022-02-25'''
| align="center" | '''1,985'''
| align="center" | '''1,066,953'''
|-
| align="center" | <span class="red">current</span>
| align="center" | '''1123'''
| align="center" | '''2022-04-25'''
| align="center" | '''1,989'''
| align="center" | '''1,079,102'''
|}
<div style="clear: both"></div>


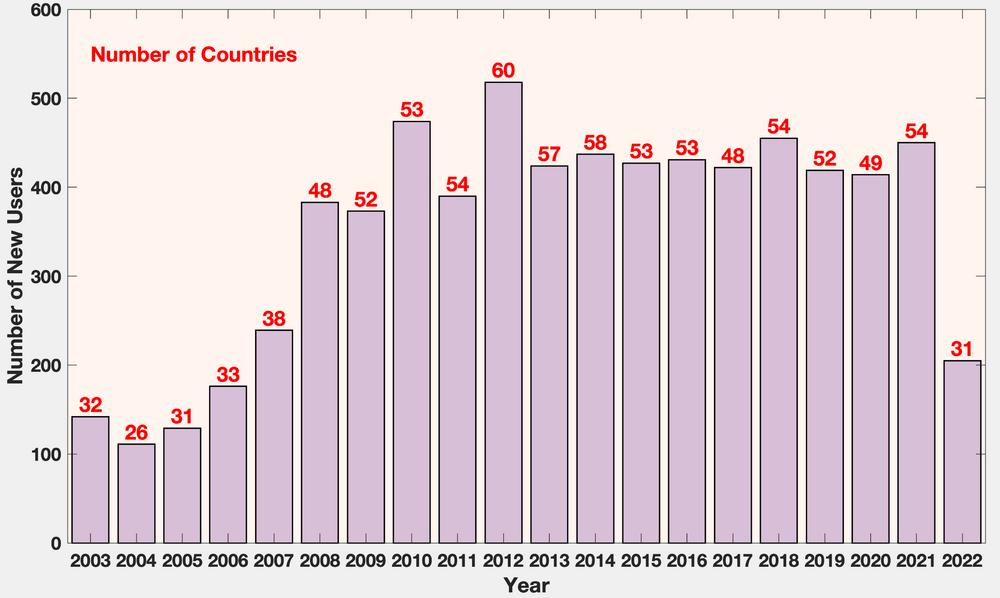
ROMS has extensive pre and post-processing software for data preparation, analysis, plotting, and visualization. The entire input and output data structure of the model is via NetCDF which facilitates the interchange of data between computers, user community, and other independent analysis software.


==ROMS Framework==
On '''May 7, 2022''', '''ROMS''' had '''6970''' registered users at [http://www.myroms.org www.myroms.org]. The histogram below shows the number of new '''ROMS''' users per year and the number of countries (<span class="red">red</span> values on top of the bar) where the new users reside.  The tally was started when '''ROMS 2.0''' was released on '''June 30, 2003'''.


<center>[[Image:framework.png]]</center>


The current ROMS framework diagram is shown above.
[[Image:roms_users.png|1000px|center]]
It illustrates various computational pathways: standalone or coupled to atmospheric and/or wave models.
 
It follows the [http://www.esmf.ucar.edu Earth System Modeling Framework (ESMF)] conventions for model coupling: <span style="color:blue">initialize</span>, <span style="color:blue">run</span> and <span style="color:blue">finalize</span>.
===ROMS Selected References===
The dynamical kernel of ROMS is comprised of four separate models including the nonlinear (<span style="color:red">NLM</span>), tangent linear (<span style="color:red">TLM</span>), representer tangent linear (<span style="color:red">RPM</span>), and adjoint (<span style="color:red">ADM</span>).
 
There are several drivers to run each model (<span style="color:red">NLM</span>, <span style="color:red">TLM</span>, <span style="color:red">RPM</span>, and <span style="color:red">ADM</span>) separately and together.
The following is an alphabetic list of '''essential publications''' describing various aspects of the '''ROMS''' algorithms:
The drivers shown in the <span style="color:blue">propagator</span> group are used for Generalized Stability Theory (GST) analysis ([[Bibliography#MooreAM_2004a |Moore et al., 2004]]) to study the dynamics, sensitivity, and stability of ocean circulations to naturally occurring perturbations, errors or uncertainties in forecasting system, and adaptive sampling.
 
The driver for adjoint sensitivities (<span style="color:blue">ADSEN</span>) computes the response of a chosen function of the model circulation to variations in all physical attributes of the system ([[Bibliography#MooreAM_2006a |Moore et al., 2006]]).
* <span id="DiLorenzo_2000a"></span>Di Lorenzo, E., A. M. Moore, H. G. Arango, B. D. Cornuelle, A. J. Miller, B. Powell, B. S. Chua, and A. F. Bennett, 2007: Weak and strong constraint data assimilation in the inverse Regional Ocean Modeling System (ROMS): Development and application for a baroclinic coastal upwelling system, ''Ocean Modelling'', '''16''', doi:10.1016/j.ocemod.2006.08.002.
It includes drivers for strong (<span style="color:blue">S4DVAR</span>, <span style="color:blue">IS4DVAR</span>) and weak (<span style="color:blue">W4DVAR</span>) constraint variational data assimilation ([[Bibliography#DiLorenzoE_2006a |Di Lorenzo et al., 2006]]).
 
A driver for <span style="color:blue">ensemble</span> prediction is available to perturb forcing and/or initial conditions along the most unstable directions of the state space using singular vectors.
* <span id="HaidvogelDB_2000a"></span>Haidvogel, D. B., H. G. Arango, K. Hedstrom, A. Beckmann, P. Malanotte-Rizzoli, and A. F. Shchepetkin, 2000: Model evaluation experiments in the North Atlantic Basin: Simulations in nonlinear terrain-following coordinates, ''Dyn. Atmos. Oceans'', '''32''', 239-281. ([http://marine.rutgers.edu/po/Papers/damee_roms1.pdf PDF])
Finally, several drivers are included in the <span style="color:blue">sanity check</span> group to test the accuracy and correctness of <span style="color:red">TLM</span>, <span style="color:red">RPM</span>, and <span style="color:red">ADM</span> algorithms.
 
* <span id="FennelK_2006a"></span>Fennel, K., J. Wilkin, J. Levin, J. Moisan, J. O'Reilly, and D. Haidvogel, 2006: Nitrogen cycling in the Middle Atlantic Bight: Results from a three-dimensional model and implications for the North Atlantic nitrogen budget, ''Global Biogeochem. Cycles'', '''20''', GB3007, doi:10.1029/2005GB002456. ([http://www.myroms.org/Papers/Fennel_etal_gbc.pdf PDF])
 
* <span id="GurolS_2014"></span>Gurol, S., A. T. Weaver, A. M. Moore, A. Piacentini, H. G. Arango, and S. Gratton, 2014: B-preconditioned minimization algorithms for variational data assimilation with the dual formulation, ''Q. J. R. Meteorol. Soc.'', '''140''', 539-556, DOI:10.1002/qj.2150.
 
* <span id=LevinJ_2020a></span>Levin, J., H.G. Arango, B. Laughlin, E. Hunter, J. Wilkin, and A.M. Moore, 2020: Observation impacts on the Mid-Atlantic Bight front and cross-shelf transportin 4D-Var ocean state estimates: Part I – Multiplatform Analysis, ''Ocean Modelling'', '''157''', doi:10.1016/j.ocemod.2020.101721.
 
* <span id="MooreAM_2021a"></span>Moore, A.M. and H.G. Arango, 2021: On the behavior of ocean analysis and forecast error covariance in the presence of baroclinic instability, ''Ocean Modelling'', '''157''', doi:10.1016/j.ocemod.2020.101733.
 
* <span id="MooreAM_2021b"></span>Moore, A.M., J. Levin, and H.G. Arango, and J. Wilkin, 2021: Assessing the performance of an ocean observing, analysis and forecast System for the Mid-Atlantic Bight using array modes, ''Ocean Modelling'', '''164''', doi:10.1016/j.ocemod.2021.101821
 
* <span id="LevinJ_2020b"></span>Levin, J., H.G. Arango, B. Laughlin, E. Hunter, J. Wilkin, and A.M. Moore, 2021: Observation impacts on the Mid-Atlantic Bight front and cross-shelf transport in 4D-Var ocean state estimates: Part II - The Pioneer Array, ''Ocean Modelling'', '''157''', doi:10.1016/j.ocemod.2020.101731.
 
* <span id="MooreAM_2004a"></span>Moore, A. M., H. G. Arango, A. J. Miller, B. D. Cornuelle, E. Di Lorenzo and D. J. Neilson, 2004: A Comprehensive Ocean Prediction and Analysis System Based on the Tangent Linear and Adjoint Components of a Regional Ocean Model, ''Ocean Modelling'', '''7''', 227-258. ([http://marine.rutgers.edu/po/Papers/Moore_2004_om.pdf PDF])
 
* <span id="MooreAM_2011a"></span>Moore, A.M., H.G. Arango, G. Broquet, B.S. Powell, A.T. Weaver, and J. Zavala-Garay, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data  assimilation systems, Part I - System overview and formulation, ''Progress in Oceanography'', '''91''', 34-49.
 
* <span id="MooreAM_2011b"></span>Moore, A.M., H.G. Arango, and G. Broquet, C. Edwards, M. Veneziani, B.S. Powell, D. Foley, J. Doyle, D. Costa, and  P. Robinson, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems, Part II: Performance and application to the California Current System, ''Progress in Oceanography'', '''91''', 50-73.
 
* <span id="MooreAM_2011c"></span>Moore, A.M., H.G. Arango, and G. Broquet, C. Edwards, M. Veneziani, B.S. Powell, D. Foley, J. Doyle, D. Costa, and P. Robinson, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems, Part III: Observation Impact and Observation Sensitivity in the California Current System, ''Ocean Modelling'', '''91''', 74-94.
 
* <span id="MooreAM_2017"></span>Moore, A.M., H.G. Arango, C.A. Edwards, 2017: Reduced-Rank Array Modes of the California Current Observing System, ''J. Geophys. Res. Ocean'', '''122''', doi:10.1002/2017JC013172.
 
* <span id="MooreAM_2020"></span>Moore, A.M., J. Zavala-Garay, H.G. Arango, C.A. Edwards, J. Anderson, and T. Hoar, 2020: Regional and basin scale applications of ensemble adjustment Kalman filter and 4D-Var ocean data assimilation systems, ''Progress in Oceanography'', '''189''', doi:10.1016/j.pocean.2020.102450.
 
* <span id="ShchepetkinAF_2003a"></span>Shchepetkin, A. F., and J. C. McWilliams, 2003: A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate, ''J. Geophys. Res.'', '''108''' (C3), 3090, doi:10.1029/2001JC001047. ([http://marine.rutgers.edu/po/Papers/2001JC001047.pdf PDF])
 
* <span id="ShchepetkinAF_2005a"></span>Shchepetkin, A. F., and J. C. McWilliams, 2005: The Regional Ocean Modeling System: A split-explicit, free-surface, topography following coordinates ocean model, ''Ocean Modelling'', '''9''', 347-404. ([http://marine.rutgers.edu/po/Papers/Shchepetkin_om05.pdf PDF])
 
* <span id="ShchepetkinAF_2008b"></span>Shchepetkin, A. F., and J. C. McWilliams, 2008: Computational kernel algorithms for fine-scale, multi-process, long-time oceanic simulations. In: ''Handbook of Numerical Analysis: Computational Methods for the Ocean and the Atmosphere'', eds. R. Temam & J. Tribbia, Elsevier Science, ISBN-10: 0444518932, ISBN-13: 978-0444518934.
 
* <span id="ShchepetkinAF_2015">Shchepetkin, A. F., 2015: An Adaptive, Courant-number-dependent Implicit Scheme for Vertical Advection in Oceanic Modeling, ''Ocean Modelling'', '''91''', 38-69, doi:10.1016/j.ocemod.2015.03.006.
 
* <span id="WarnerJC_2013"></span>Warner, J. C., Z. Defne, K. Hass, and H. G. Arango, 2013: A wetting and drying scheme for ROMS, ''Computers & Geosciences'', '''58''', 54-61, 10.1016/j.cageo.2013.05.004.
 
* <span id="WarnerJC_2013"></span>Warner, J.C., W.R. Geyer, and H.G. Arango, 2010: Using composite grid approach in complex coastal domain to estimate estuarine residence time, ''Computer and Geosciences'', '''36''', 921-935, doi:10.1016/j.cageo.2009.11.008.
 
* <span id="WarnerJC_2006a"></span>Warner, J. C., C. R. Sherwood, R. P. Signell, C. K. Harris, and H. G. Arango, 2008: Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model, ''Computers & Geosciences'', '''34''', 1284-1306.
 
* <span id="WarnerJC_2005a"></span>Warner, J. C., C. R. Sherwood, H. G. Arango, and R. P. Signell, 2005a: Performance of four turbulence closure methods implemented using a generic length scale method, ''Ocean Modelling'', '''8''', 81-113. ([http://marine.rutgers.edu/po/Papers/Warner_2004_om.pdf PDF])
 
* <span id="WilkinJL_2006a"></span>Wilkin, J. L., 2006: The summer time heat budget and circulation of southeast New England shelf, ''J. Phys. Oceanog.'', '''36''', 1997-2011. ([http://marine.rutgers.edu/%7Ewilkin/Wilkin_CBLAST_JPO2006.pdf PDF])

Latest revision as of 13:21, 19 May 2022

ROMS History

In the fall of 1995, Hernan G. Arango (hereafter HGA) started working at the Ocean Modeling Lab (OML), Institute of Marine and Coastal Sciences (IMCS), Rutgers University. His first assignment from OML's group leader Dale B. Haigvogel (hereafter DBH) was to work on the classic baroclinic, wind-driven, double gyre problem with the now-extinct S-Coordinate Rutgers University Model (SCRUM, Song and Haidvogel, 1994), which was derived from SPEM (Semi-spectral Primitive Equation Model; Haidvogel et al., 1991). The double-gyre application is affectionately known as Big Bad Basin (nowadays, BASIN test case) by several OML modelers because of its stability issues in long simulations. After a couple of months of struggling with the BASIN problem, HGA decided to rewrite SCRUM from scratch and modify its numerical kernel, including time-stepping, advection schemes, and implementing a split-explicit treatment coupling between barotropic (fast) and barotropic (slow) governing equations in collaboration with OML's scientists Robert J. Chant and Katherine S. Hedström. In addition, a complete overhaul of the model metadata, input, and output files with NetCDF format. And voilà, the BASIN application ran successfully for several years. The new model became SCRUM version 3.0, which later evolved to SCRUM 4.0 and then becomes the Regional Ocean Modeling System (ROMS). The acronym ROMS was inspired by the Regional Atmospheric Modeling System (RAMS). Thus, at the time, there was a regional numerical model for the atmosphere and ocean with similar acronyms.

In 1998, James C. McWilliams (hereafter, JCM) started looking for a regional ocean model for the U.S. West Coast and contacted DBH for possible collaborations. As a result, DBH and HGA traveled to Los Angeles, to meet at University of California, Los Angeles (UCLA) with JCM and Alexander F. Shchepetkin (hereafter AFS) or just Sasha, as the ROMS VIPs know him. The expectation that HGA and AFS would get along was very low. However, their mutual respect, skills, and friendship grew. As a result, and to the benefit of the ocean modeling community, ROMS was officially born. Their first task was to improve its efficiency by implementing a multi-threaded parallel version of its numerical kernel using the shared-memory paradigm native to the IRIX operating system available on SGI supercomputers of the time. The shared-memory compiling directives evolved later to the portable OpenMP standard implementation in ROMS. Moreover, AFS began looking at the ensemble code and started counting operations; multiplications replaced unnecessary divisions when appropriate, and DO-loops were reorganized and pipelined to reduce memory hits. HGA learned how to count operations and analyzed optimized Fortran code, which was available at the time, to minimize the need for automatic optimization. As a result, the ROMS code was very efficient and fast. Nowadays, ROMS can be compiled with aggressive Fortran optimization flags. Of course, users need to be aware that the bold optimization flags in some compilers could compromise the numerical IEEE floating-point precision, and new flags are required to retain it, which may slow down the computations.

In 2000, Terri Paluszkiewicz from the Office of Naval Research (ONR) approached HGA and JCM about funding opportunities to develop the next generation of a regional, high-resolution ocean model with accurate numerical algorithms and data assimilation capabilities. As a result, ONR started funding ROMS development separately to Rutgers (data assimilation and adjoint-based algorithms, applications, maintenance, and community outreach) and UCLA (numerical algorithms and applications). Then, HGA suggested to ONR that a redesign of ROMS was required, and a team of experts was needed to do variational data assimilation correctly. During his years at Harvard, HGA had the opportunity to meet Andrew M. Moore (hereafter, AMM), now at the University of California, Santa Cruz (UCSC), and work with Arthur J. Miller (hereafter, AJM) from the Scripps Institute of Oceanography (SIO). AMM is an expert on adjoint-based modeling and applications. Therefore, the ROMS data assimilation team included AMM, HGA, AJM, collaborator Bruce D. Cornuelle (hereafter, BDC), and Ph. D. student Emanuele Di Lorenzo (hereafter, EDL), and Douglas J. Neilson (Hereafter, DJW). ONR also funded UCSC and SIO separately for this work. Thus, it started a very successful collaboration with several peer-reviewed publications in journals and books. The chemistry between the ROMS Data Assimilation (ROMS-DA) group was extraordinary, with lots of fun, good food, and great wine-tasting parties.

AdjointGroup.jpg
ROMS Adjoint Group: Back, left to right: Arthur J. Miller, Andrew M. Moore, Bruce D. Cornuelle, and Douglas J. Neilson. Front: Hernan G. Arango and Emanuel Di Lorenzo.

AMM and HGA frequently traveled to Scripps, in La Jolla, for an intense week-long perturbation, tangent linear model (TLM) and adjoint model (ADM) code writing. AMM was the master teaching and directing the monkies on how to write ROMS-TL and ROMS-AD codes. The TLM and ADM were hand-coded from the discrete nonlinear (NLM) code using the recipes of Giering and Kaminski (1998). Therefore, any change to its dynamical and numerical kernels will affect the symmetry of the TLM and ADM operators. Moreover, the resulting discrete adjoint is exact and is defined relative to the inner product that prescribes the L2-norm. The finite-amplitude, tangent linear code for the Representer model (RPM) was later derived from the TLM. The RPM is used in the indirect, representer-based approach for 4-Dimensional Variational (4D-Var) data assimilation.

To be continued ...

ROMS Releases

The following table shows information about the infrequent tagged ROMS releases showing its evolution and expansion. It was redesigned completely starting with version ROMS 2.0 and written in Fortran-1990 standard with modules with the derived-type objects with dynamical allocation, and managed with svn repositories instead of cvs. Some features of Fortran-1995 and Fortran-2003 standards were introduced later when available in mostly all compilers. The perturbation Tangent Linear Model (TLM), finite-amplitude Tangent Linear (Representer) Model (RPM), and adjoint model (ADM) were released in version ROMS 2.3.


Tag Version svn Revision Release Date Number of Files Lines of Code
1.1.0 cvs -r 1.1.0 1999-01-20 125 44,639
1.2.0 cvs -r 1.2.0 1999-01-25 130 46,905
1.3.0 cvs -r 1.3.0 1999-03-15 131 47,931
1.4.0 cvs -r 1.4.0 1999-06-20 146 49,466
1.5.0 cvs -r 1.5.0 2000-02-10 145 56,118
1.6.0 cvs -r 1.6.0 2000-01-29 144 56,066
1.6.1 cvs -r 1.6.1 2000-03-06 144 56,123
1.6.2 cvs -r 1.6.2 2000-03-17 144 56,283
1.7.0 cvs -r 1.7.0 2001-01-19 165 63,652
1.7.1 cvs -r 1.7.1 2001-02-01 165 63,573
1.7.2 cvs -r 1.7.2 2001-04-17 173 66,324
1.8.0 cvs -r 1.8.0 2002-01-11 175 67,999
2.0 2 2003-06-30 232 95,836
2.1 3 2004-05-05 253 117,956
2.2 4 2005-05-26 297 158,176
2.3 8 2007-02-06 1,122 399,457
3.0 36 2007-04-27 1,313 460,643
3.1 166 2008-03-17 1,345 470,110
3.2 338 2009-03-25 1,428 549,318
3.3 432 2009-12-26 1,559 603,578
3.4 550 2011-04-19 1,583 643,878
3.5 568 2011-09-21 1,582 648,098
3.6 656 2013-04-18 1,638 684,351
3.7 974 2019-07-25 1,784 844,948
3.8 995 2020-01-09 1,799 848,245
3.9 1054 2021-03-06 1,909 884,508
4.0 1108 2022-02-25 1,985 1,066,953
current 1123 2022-04-25 1,989 1,079,102


On May 7, 2022, ROMS had 6970 registered users at www.myroms.org. The histogram below shows the number of new ROMS users per year and the number of countries (red values on top of the bar) where the new users reside. The tally was started when ROMS 2.0 was released on June 30, 2003.


roms users.png

ROMS Selected References

The following is an alphabetic list of essential publications describing various aspects of the ROMS algorithms:

  • Di Lorenzo, E., A. M. Moore, H. G. Arango, B. D. Cornuelle, A. J. Miller, B. Powell, B. S. Chua, and A. F. Bennett, 2007: Weak and strong constraint data assimilation in the inverse Regional Ocean Modeling System (ROMS): Development and application for a baroclinic coastal upwelling system, Ocean Modelling, 16, doi:10.1016/j.ocemod.2006.08.002.
  • Haidvogel, D. B., H. G. Arango, K. Hedstrom, A. Beckmann, P. Malanotte-Rizzoli, and A. F. Shchepetkin, 2000: Model evaluation experiments in the North Atlantic Basin: Simulations in nonlinear terrain-following coordinates, Dyn. Atmos. Oceans, 32, 239-281. (PDF)
  • Fennel, K., J. Wilkin, J. Levin, J. Moisan, J. O'Reilly, and D. Haidvogel, 2006: Nitrogen cycling in the Middle Atlantic Bight: Results from a three-dimensional model and implications for the North Atlantic nitrogen budget, Global Biogeochem. Cycles, 20, GB3007, doi:10.1029/2005GB002456. (PDF)
  • Gurol, S., A. T. Weaver, A. M. Moore, A. Piacentini, H. G. Arango, and S. Gratton, 2014: B-preconditioned minimization algorithms for variational data assimilation with the dual formulation, Q. J. R. Meteorol. Soc., 140, 539-556, DOI:10.1002/qj.2150.
  • Levin, J., H.G. Arango, B. Laughlin, E. Hunter, J. Wilkin, and A.M. Moore, 2020: Observation impacts on the Mid-Atlantic Bight front and cross-shelf transportin 4D-Var ocean state estimates: Part I – Multiplatform Analysis, Ocean Modelling, 157, doi:10.1016/j.ocemod.2020.101721.
  • Moore, A.M. and H.G. Arango, 2021: On the behavior of ocean analysis and forecast error covariance in the presence of baroclinic instability, Ocean Modelling, 157, doi:10.1016/j.ocemod.2020.101733.
  • Moore, A.M., J. Levin, and H.G. Arango, and J. Wilkin, 2021: Assessing the performance of an ocean observing, analysis and forecast System for the Mid-Atlantic Bight using array modes, Ocean Modelling, 164, doi:10.1016/j.ocemod.2021.101821
  • Levin, J., H.G. Arango, B. Laughlin, E. Hunter, J. Wilkin, and A.M. Moore, 2021: Observation impacts on the Mid-Atlantic Bight front and cross-shelf transport in 4D-Var ocean state estimates: Part II - The Pioneer Array, Ocean Modelling, 157, doi:10.1016/j.ocemod.2020.101731.
  • Moore, A. M., H. G. Arango, A. J. Miller, B. D. Cornuelle, E. Di Lorenzo and D. J. Neilson, 2004: A Comprehensive Ocean Prediction and Analysis System Based on the Tangent Linear and Adjoint Components of a Regional Ocean Model, Ocean Modelling, 7, 227-258. (PDF)
  • Moore, A.M., H.G. Arango, G. Broquet, B.S. Powell, A.T. Weaver, and J. Zavala-Garay, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems, Part I - System overview and formulation, Progress in Oceanography, 91, 34-49.
  • Moore, A.M., H.G. Arango, and G. Broquet, C. Edwards, M. Veneziani, B.S. Powell, D. Foley, J. Doyle, D. Costa, and P. Robinson, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems, Part II: Performance and application to the California Current System, Progress in Oceanography, 91, 50-73.
  • Moore, A.M., H.G. Arango, and G. Broquet, C. Edwards, M. Veneziani, B.S. Powell, D. Foley, J. Doyle, D. Costa, and P. Robinson, 2011: The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems, Part III: Observation Impact and Observation Sensitivity in the California Current System, Ocean Modelling, 91, 74-94.
  • Moore, A.M., H.G. Arango, C.A. Edwards, 2017: Reduced-Rank Array Modes of the California Current Observing System, J. Geophys. Res. Ocean, 122, doi:10.1002/2017JC013172.
  • Moore, A.M., J. Zavala-Garay, H.G. Arango, C.A. Edwards, J. Anderson, and T. Hoar, 2020: Regional and basin scale applications of ensemble adjustment Kalman filter and 4D-Var ocean data assimilation systems, Progress in Oceanography, 189, doi:10.1016/j.pocean.2020.102450.
  • Shchepetkin, A. F., and J. C. McWilliams, 2003: A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate, J. Geophys. Res., 108 (C3), 3090, doi:10.1029/2001JC001047. (PDF)
  • Shchepetkin, A. F., and J. C. McWilliams, 2005: The Regional Ocean Modeling System: A split-explicit, free-surface, topography following coordinates ocean model, Ocean Modelling, 9, 347-404. (PDF)
  • Shchepetkin, A. F., and J. C. McWilliams, 2008: Computational kernel algorithms for fine-scale, multi-process, long-time oceanic simulations. In: Handbook of Numerical Analysis: Computational Methods for the Ocean and the Atmosphere, eds. R. Temam & J. Tribbia, Elsevier Science, ISBN-10: 0444518932, ISBN-13: 978-0444518934.
  • Shchepetkin, A. F., 2015: An Adaptive, Courant-number-dependent Implicit Scheme for Vertical Advection in Oceanic Modeling, Ocean Modelling, 91, 38-69, doi:10.1016/j.ocemod.2015.03.006.
  • Warner, J. C., Z. Defne, K. Hass, and H. G. Arango, 2013: A wetting and drying scheme for ROMS, Computers & Geosciences, 58, 54-61, 10.1016/j.cageo.2013.05.004.
  • Warner, J.C., W.R. Geyer, and H.G. Arango, 2010: Using composite grid approach in complex coastal domain to estimate estuarine residence time, Computer and Geosciences, 36, 921-935, doi:10.1016/j.cageo.2009.11.008.
  • Warner, J. C., C. R. Sherwood, R. P. Signell, C. K. Harris, and H. G. Arango, 2008: Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model, Computers & Geosciences, 34, 1284-1306.
  • Warner, J. C., C. R. Sherwood, H. G. Arango, and R. P. Signell, 2005a: Performance of four turbulence closure methods implemented using a generic length scale method, Ocean Modelling, 8, 81-113. (PDF)
  • Wilkin, J. L., 2006: The summer time heat budget and circulation of southeast New England shelf, J. Phys. Oceanog., 36, 1997-2011. (PDF)
Retrieved from "https://www.myroms.org/wiki/index.php?title=Regional_Ocean_Modeling_System_(ROMS)&oldid=6532"