Opened 10 years ago
Closed 10 years ago
#702 closed upgrade (Done)
IMPORTANT: Big update to 4D-Var Data Assimilation Algorithms
| Reported by: | arango | Owned by: | arango |
|---|---|---|---|
| Priority: | major | Milestone: | Adjoint Based Algorithms |
| Component: | Adjoint | Version: | 3.7 |
| Keywords: | Cc: |
Description
This is a very important update to the ROMS 4D-Var algorithms. It includes new options and several bug corrections. We have been working and refining these algorithms for the last couple of years.
WARNING: If you update to this version, you need to recompute the error covariance normalization coefficients for your 4D-Var application. This is extremely important since several bugs were corrected in the computation of the normalization coefficients. It is the user responsibility to make sure that this takes place in order to have the correct 4D-Var solution with this ROMS update.
What is New:
- Several new C-preprocessing options are introduced:
- BEOFS_ONLY: Use to compute the EOFs of the background error covariance.
- BNORM: Use the background normalization of the Hessian singular vectors in various adjoint-based algorithms.
- BGQC: Use for background quality control of observations.
- EVOLVED_LCZ: Use to compute 4D-Var evolved Hessian singular vectors.
- GEOPOTENTIAL_HCONV: Use to perform horizontal convolution of error covariance along geopotential surfaces in the 4D-Var algorithms.
- LCZ_FINAL: Use to compute 4D-Var Hessian singular vectors.
- RPCG: Use to activate the Restricted B-preconditioned Lanczos (RBLanczos) minimization method in the 4D-Var dual fourmulation algorithms (4D-PSAS and R4D-Var).
- TIME_CONV: Use to activate weak-contraint time convolution in the 4D-Var dual formulation algorithms (4D-PSAS and R4D-Var).
- BEOFS_ONLY: Use to compute the EOFs of the background error covariance.
- Added the option to perform a background quality control the observations in terms of the state variables index or the observation provenance for a particular state variable. It is activated with the BGQC option. Several new parameters are added to input script s4dvar.in to achieve this quality control:
! Select flag for BackGround Quality Control (BGQC) of observations: ! ! [1] Quality control in terms of state variable indices ! [2] Quality control in terms of observation provenance bgqc_type == 1 ! If BGQC is in terms of state variables, set number of standard deviations ! threshold to use in the quality control rejection of observations. ! ! Use a large value (say, 1.0d+5) if you do not want to reject observations ! associated with a particular state variable. ! ! Use a small value (typically, 4 standard deviations) to perform quality ! control of observations for a particular state variable. S_bgqc(isFsur) == 1.0d+5 ! free-surface S_bgqc(isUbar) == 1.0d+5 ! 2D U-momentum S_bgqc(isVbar) == 1.0d+5 ! 2D V-momentum S_bgqc(isUvel) == 1.0d+5 ! 3D U-momentum S_bgqc(isVvel) == 1.0d+5 ! 3D V-momentum S_bgqc(isTvar) == 4.0d0 4.0d0 ! 1:NT tracers ! If BGQC is in terms of observation provenance, set number of standard ! deviations threshold to use in the quality control rejection of ! observations. ! ! Use a small value (say, 4 standard deviations) to perform quality ! control for the desired observation provenance(s). ! ! Nprovenance: Number of observation provenances to quality control ! Iprovenance: Observation provenance indices to process [1:Nprovenance] ! P_bgqc: Standard deviation threshold [1:Nprovenance] Nprovenance == 2 Iprovenance == 6 7 ! ARGO Temperature and Salinity P_bgqc == 4.0d0 4.0d0
- Add the option to include temporal decorrelation scales in the model error covariance for the 4D-Var dual formulation, weak-constraint algorithms (4D-PSAS and R4-Var). It is activated with the TIME_CONV option. Recall that both 4D-PSAS (W4DPSAS option) and R4D-Var (W4DVAR option) can be run in either strong-constraint or week-constraint modes. For strong-constraint, the user needs to set NADJ to the same value of NTIMES in ocean.in:
! Time-Stepping parameters. NTIMES == 192 ... ! Output tangent linear and adjoint models parameters. ... NADJ == 192 ! strong constraintConversely in weak-constraint configurations, NADJ needs to be a multiple of NTIMES. For example:! Time-Stepping parameters. NTIMES == 192 ... ! Output tangent linear and adjoint models parameters. ... NADJ == 48 ! weak constraintThe parameters for the weak constraint time correlations are specified in input script s4dvar.in:! Model error covariance: temporal decorrelation scales (days). ! This scales are only used in weak-constraint data assimilation. TdecayM(isFsur) == 1.0d0 ! free-surface TdecayM(isUbar) == 1.0d0 ! 2D U-momentum TdecayM(isVbar) == 1.0d0 ! 2D V-momentum TdecayM(isUvel) == 1.0d0 ! 3D U-momentum TdecayM(isVvel) == 1.0d0 ! 3D V-momentum TdecayM(isTvar) == 1.0d0 1.0d0 ! 1:NT tracers
- A new 4D-Var minimization solver was added for the dual formulation (space spanned by the observation vector) drivers. Use the RPCG option to activate it in either 4D-PSAS or R4D-Var. It is named as the Restricted B-preconditioned Lanczos (RBLanczos) algorithm by Gurol et al. (2014). It is mathematically equivalent to the Restricted B-preconditioned Conjugate Gradient (RBCG) used in the primal formulation (space spanned by the model state vector). More importantly, it has similar convergence properties as the primal formulation minimization solvers making weak-constraint 4D-Var very affordable. For example, for a weak-constraint 4D-PSAS in the WC13 test application we get:
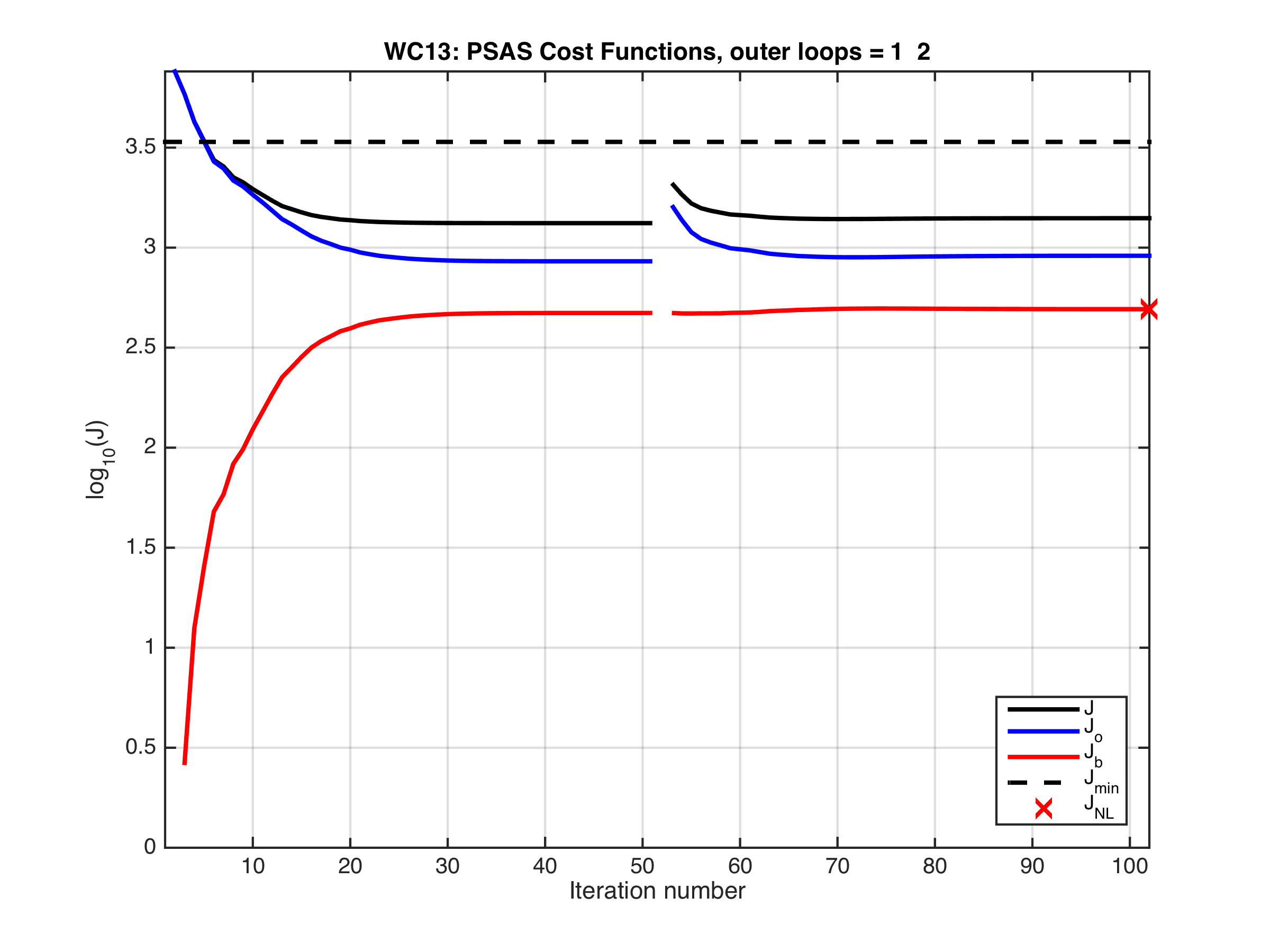
The figure shows the cost functions for two outer loops with 51 inner loops each (iterations). Both outer loops are plotted continuously to facilitate comparisons. Notice that the cost functions converge rapidly around 20 interactions in the first outer loop and just 10 iterations in the second outer loop.
The RBLanczos algorithm (rpcg_lanczos.F) was very difficult to code. It gets quite complex when adding the augmented terms so can be used with multiple outer loops applications. Many thanks to Selime Gürol (CERFACS) and Andy Moore (UCSC) for helping us code this tricky solver. Please check the following paper to learn more about RBLanczos:
Gürol, S., A.T. Weaver, A.M. Moore, A. Piacentini, H.G. Arango, S. Gratton, 2014: B-preconditioned minimization algorithms for data assimilation with the dual formulation, Q. J. R. Meteorol. Soc., 140, 539-556.
- The routine normalization.F which computes the background and model error covariance (B and Q, respectively) normalization coefficient was revised and several bugs were corrected. These coefficients ensure that the diagonal elements of B and Q are equal to unity. We can use the exact (Nmethod=0; expensive) or approximated randomization (Nmethod=1; cheaper) methods. They just need to be computed once for a particular set of decorrelation scales. BEWARE, since this routine changed a lot, users need to recompute these coefficients for their 4D-Var application when updating to this version of ROMS.
- Added several new files including ad_force_dual.F, comp_Jb0.F, lanc_resid.F, rpcg_lanczos.F, sum_imp.F, time_corr.F, wrt_aug_imp.F, and wrt_evolved.F. Also, numerous updates to several subroutines were carry out.
Many thanks to Andy Moore for his help in coding and testing all these algorithms. We have been talking about this update for the last couple of years and have so many research versions of the code that were becoming unmanageable.
