Analysis-Forecast Cycle Observation Impacts
The procedure for computing the observation impacts during the forecast cycle is a little more involved than that for the analysis cycle. However, a separate ROMS driver exists for this. To help illustrate the procedure involved, consider the typical analysis-forecast cycle shown schematically below.
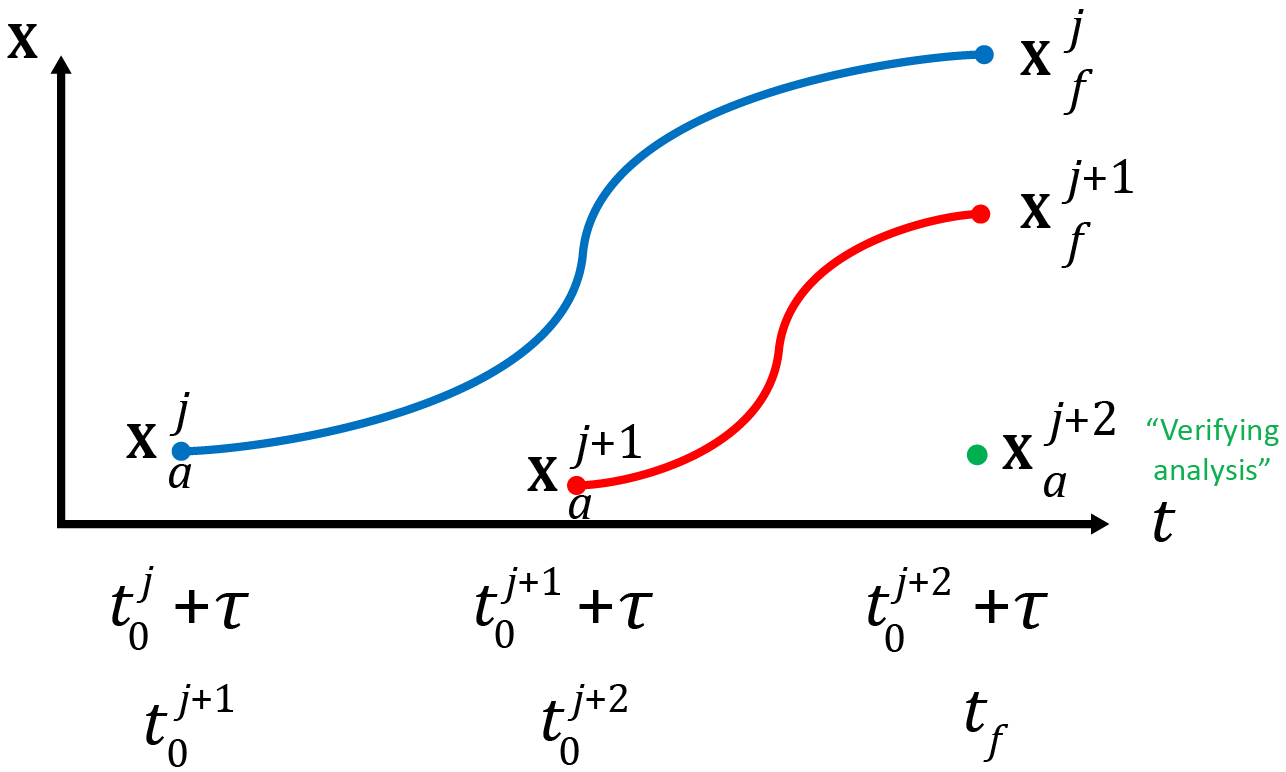
In the figure above, each analysis cycle is assumed to be of length and analysis cycle spans the interval. The circulation estimate at time (i.e. the end of analysis cycle ) is denoted as and is the initial condition for the forecast spanning the next analysis interval . In the figure it is assumed, for convenience only, that the forecast duration is an integer multiple of , but this does not have to be the case, and the code is set up to handle analysis and forecast cycles that are different lengths. Figure 1 shows the analyses and forecasts that result from three adjacent analysis cycles, namely cycles , and cycle . The analysis at the end of cycle is used as the initial condition for the forecast of duration that terminates at time , the end of analysis cycle . Similarly, the analysis at the end of cycle is used as the initial condition for the forecast of duration and also terminates at time , the end of analysis cycle . After sufficient time has elapsed, a new analysis will be computed at this time. Since represents our best estimate of the ocean circulation at time it can be used to quantify the veracity of the forecasts and . For this reason, is usually referred to as the “verifying analysis.” However, as discussed shortly, other sources of information can be used to verify the forecasts, such as new or independent observations.
It should be clear from the figure that the forecast benefits from the observations assimilated into the model during analysis cycle (i.e. during the interval ). Therefore, providing that and are subject to identical surface forcing and open boundary conditions during the interval , any differences in forecast error must be associated with the observations assimilated into the model during the interval .
Forecast Error Metrics
As in the case of the analysis cycle observation impacts described above, the impact of the observations during the forecast cycle is computed for a specific metric, in this case a metric of the forecast error. The methodology will be described first for a standard generic quadratic forecast error metric given by:
| (1) |
where denotes the forecast state-vector, denotes the true state-vector, and is a weight matrix. For example, if is a diagonal matrix with elements equal to 1 corresponding to all surface temperature grid points, and zero elsewhere, then would represent the sum of the squared errors in SST. Forecast error metrics of the form (1) are very common in numerical weather prediction and oceanography, so (1) is a good starting point.
In the figure there are two forecasts of interest: initialized at the end of analysis cycle at time , and initialized at the end of analysis cycle at time . At time the error in forecast is given by , while the error in is given by . As noted above, if and are subject to identical surface forcing and open boundary conditions during the interval , then the difference in forecast error is due solely to the difference in the forecast initial conditions due to the observations assimilated during analysis cycle spanning the interval . (The more realistic case where the two forecasts are subject to different surface forcing fields is addressed below in the “step-by-step procedure” notes). Specifically, if the observations assimilated during cycle lead to an improvement in the forecast skill (i.e. ), while if the observations assimilated during cycle have degraded the forecast (i.e. ). While this convention may seem counter-intuitive, it is the convention used in the numerical weather prediction literature, so it seems prudent to adopt it here.

![[t_{0}^{j},t_{0}^{j}+\tau ]](https://www.myroms.org/myroms.org/v1/media/math/render/svg/4875462b6bcf6997a0bc290d70d34d26ff400086)






![[t_{0}^{{j+1}},t_{0}^{{j+1}}+\tau ]](https://www.myroms.org/myroms.org/v1/media/math/render/svg/80b866aae3052d01acd3822cf99549c4cd8fb48d)






![[t_{0}^{{j+2}},t_{0}^{{j+2}}+\tau ]](https://www.myroms.org/myroms.org/v1/media/math/render/svg/6a7b3f682200e6f6166806c3b5c536d2d2716757)














